時系列データの未来予測 - 航空機乗客数の予測
AIゆめ
LSTMモデルによる未来予測は、本ページに示すようにトレンドがある時系列データであっても、高精度に予測することが可能であり、多次元化も容易に行えますので、需要解析など複数要素が絡む問題解決に適しています。製造業・非製造業に拘わらず、「自社の問題解決に応用できるのではないか?」と思われた方は、
ネオラクス・メール送信フォーム からお気軽にご相談ください。AI技術を用いて、世の中にある様々な問題の解決に貢献して行きたいと思います。なお、多要素が絡んだより複雑なモデルである二次元Autoencoderモデルを、
高精度な気温予測 - 二次元Autoencoderモデル のページに紹介していますので併せてご覧ください。
各モデルの解説
本ページで使用するモデルについて、簡単に解説する。LSTMモデルは、チャットなどで使用されることが多く、次に来る単語を予測するモデルに使用されることが多いAIモデルの一つであり、定常、非定常を問わず適用可能な手法である。ARモデル、ARIMAモデル、SARIMAモデルなどの統計解析手法は、元々、定常な周期性の強い時系列データの解析用に開発された手法である。以下、各モデルについて簡単に説明する。
LSTMモデル
AIモデルを用いて時系列データの未来を予測するLSTMモデルは、
時系列予測:TensorFlowチュートリアル で示されているように、気温や風速など一定の時刻幅と、次の時刻の目標値(今回の場合は気温)のデータセットを教師データとして学習させる方法が一般的であり、下図に示すようなデータを生成することから始める。即ち、\([x_{i}, x_{i+1}, x_{i+2},...,x_{i+T-3}, x_{i+T-2}, x_{i+T-1}]\)という\(i\)行のデータに対応するラベルが、\(x_{i+T+H-1}\)になっている。ここで、\(N\)はデータ\(x\)の個数、\(T\)はタイムステップ幅(LSTMが記憶する離散時時間幅)、\(H\)は何ステップ先を予測するかを表すステップ数(通常は1ステップ先を予測するので(\(H=1\))。
\(
\begin{align*}
i=0: [ &[x_0, x_1, x_2, &..., x_{T-3}, x_{T-2}, x_{T-1}], &→ &[x_{T+H-1},\\
i=1: &[x_1, x_2, x_3, &..., x_{T-2}, x_{T-1}, x_{T}], &→ &x_{T+H},\\
i=2: &[x_2, x_3, x_4, &..., x_{T-1}, x_{T}, x_{T+1}], &→ &x_{T+H+1},\\
&...,\\
i=T-1: &[x_{T-1}, x_T, x_{T+1}, &..., x_{2T-4}, x_{2T-3}, x_{2T-2}], &→ &x_{2T+H-2},\\
i=T: &[x_{T}, x_{T+1}, x_{T+2}, &..., x_{2T-3}, x_{2T-2}, x_{2T-1}], &→ &x_{2T+H-1},\\
i=T+1: &[x_{T+1}, x_{T+2}, x_{T+3}, &..., x_{2T-2}, x_{2T-1}, x_{2T}], &→ &x_{2T+H},\\
&...,\\
i=N-T-H: &[x_{N-T-H}, x_{N-T-H+1}, &..., x_{N-H-2}, x_{N-H-1}] ] &→ &x_{N-1}]\\
\end{align*}
\)
このように、\((N-T-H+1,T)\)テンソルの\(x\)データ(矢印の左側)と、これに対応する\((N-T-H+1)\)ベクトルの\(y\)ラベル(矢印の右側)を作成し、このデータセットから学習することになる。また、通常の統計モデルに比較して。LSTMモデルで予測する場合の注意点が3点ある。一つ目は、データ数としてある程度の長さ(数百~数千のオーダー)が必要である点である。上記の航空機乗客数のデータは12年間の月毎の乗客数であるため144データしかない。そこで、補間して日毎として与えているため、全データ数は4,353データである。二つ目は、精度を上げるためにはタイムステップ幅(LSTMが記憶する離散時時間幅)はある程度長くしなければならないことであり、ここでは128日とした。三つ目は、年や月ごとの変化(本来の日々のデータがある場合は日々の変化)などを精度よく捉えるために、単に年月日が入った列を用意するのではなく、下記のように'年','月','日'のデータを用意する必要がある点である。このような準備をすることにより、格段に精度が向上する。
#年月日をカラムに分ける
df['Year'] = df.index.year
df['Month'] = df.index.month
df['Day'] = df.index.day
df = df.astype('float64')
そして、正規化を行った後、訓練データ(df_train:評価データと予測データを除くデータ)、評価データ(df_val)360日分、予測確認データ(df_pred)360日分に分割する。時系列解析なのでシャッフルは行わない。訓練データで訓練を行い、1エポックごとに評価データのmse(平均二乗誤差)が最小になるよう学習を続ける。そして、予測確認データは、予測値の精度評価のためだけに使用するので、訓練では全く使用しない。正規化においては、全データが0~1の範囲に入るようにしたが、-1~1の範囲でも良いし、標準偏差で割って±1の範囲から多少はみ出すような設定でも問題はない。
#正規化を行う
df_min = df.min()
df_norm = df.max() - df_min
df = ( df - df_min ) / df_norm
#train,test,valに分割する
df_num = len(df)
df_train = df[0:int(df_num*0.8)]
df_val = df[int(df_num*0.8):int(df_num*0.9)]
df_pred = df[int(df_num*0.9):]
ARモデル(Auto Regression Model:自己回帰モデル)
ARモデル(Auto Regression Model:自己回帰モデル)については、
姿勢推定 - PoseEstimation のページでも解説したが、AIモデル構築のため、膨大な周期性の強い時系列データの中から、効果的な特徴量(目的関数の特徴を説明する次元を落とした量)を抽出するための有効な手法の一つであることを解説した。時刻\(t\)における変数\(y_t\)は、ARモデルでは以下のように表現される。
\begin{align}
y_t = \sum_{ i = 1 }^{ P } φ_i y_{t-i} + ε_t + c \tag{1}
\end{align}
ここで、\(φ_i\)はARパラメータ、\(ε_t\)は白色雑音(ホワイトノイズ)、\(c\)は定数である。即ち、このモデルは、時刻\(t\)における変数\(y_{t}\)が、現在より\(i\)時刻前の過去の自分の値、ホワイトノイズ、定数の合計で示されるというモデルである(\(i=1,2,3,...,P\))。
SARIMAモデル
ARIMAモデル(Auto-Regressive Integrated Moving Average Model:自己回帰和分移動平均モデル)に季節性の影響を考慮したSARIMAモデル(Seasonal ARIMA Model:季節性を考慮した自己回帰和分移動平均モデル)も比較対象とした。SARIMAモデルのパラメータとしては、非季節性パラメータ\((p,d,q)\)と季節性パラメータ\((P, D, Q, m)\)がある。ここで、\((p,d,q)\)は、非季節性を考慮しないARIMAモデルのパラメータと同じで、それぞれ、自己回帰(AR)パラメータ、(I)和分パラメータ、(MA)移動平均パラメータに該当し、これと同様に季節性パラメータ\(P, D, Q\)と、季節性の周期\(m\)がある。今回の例では12ヶ月周期の影響が強いので\(m=12\)に設定する。他のパラメータ設定に関しては、
Pythonで時系列解析・超入門(その3)ARIMA系モデルで予測する方法 のページを参考に、手動設定と自動設定を試した。
LSTMモデルによる未来予測結果
今回使用したLSTMモデルは下図に示すような二層LSTMモデルである。第一層目では、第二層目で使用する配列\(T\)の部分の情報が必要であるため'return_sequences=True'とし、第二層目ではこの情報は必要ないので'return_sequences=False'としている。なお、一層LSTMモデルでも、そこそこ良い結果は得られているが、二層モデルの方が少し優れていたので二層LSTMモデルの結果のみ示す。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 128, 128) 68096
lstm_1 (LSTM) (None, 64) 49408
dense (Dense) (None, 1) 65
=================================================================
Total params: 117,569
Trainable params: 117,569
Non-trainable params: 0
_________________________________________________________________
model = tf.keras.Sequential([
# 入力層
tf.keras.layers.InputLayer(input_shape=(TIME_STEPS, COLUMN_NUM)),
# LSTM層
tf.keras.layers.LSTM(128, return_sequences=True),
tf.keras.layers.LSTM(64, return_sequences=False),
# Shape => [batch, time, features]
tf.keras.layers.Dense(1)
])
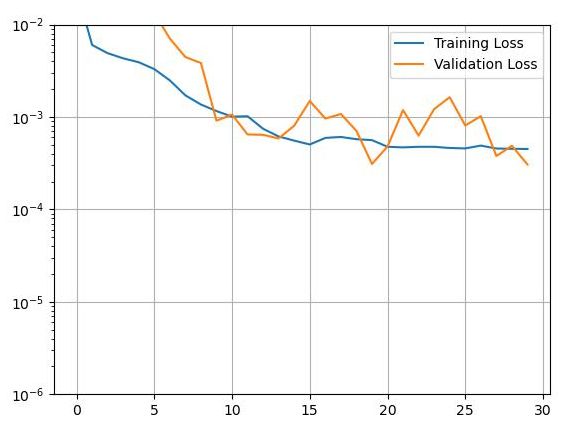
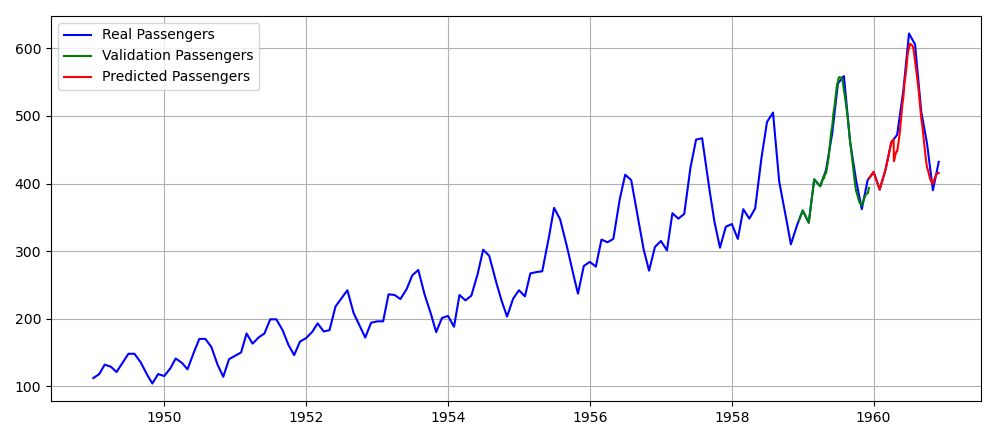
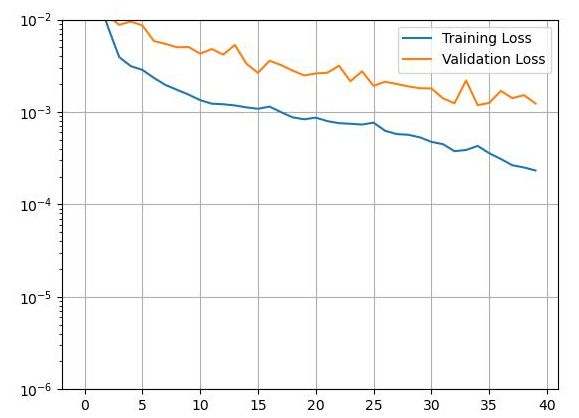
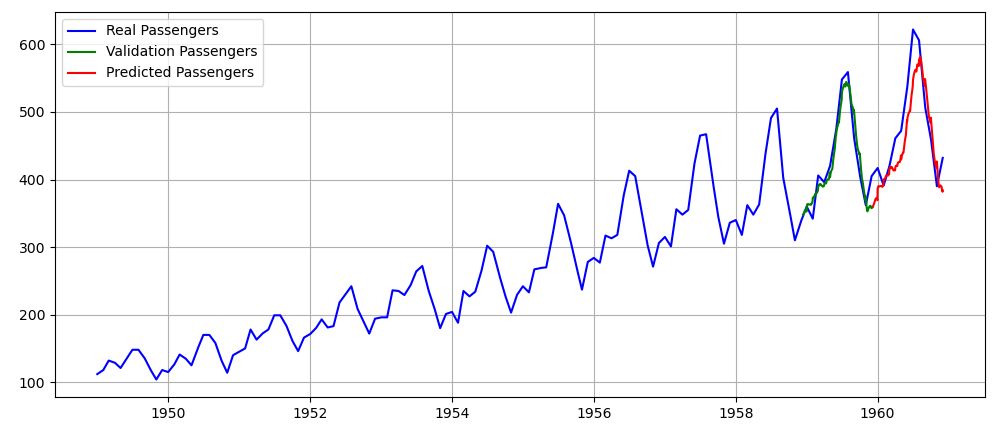
図1および図2に、二層LSTMモデルの機械学習の進行状況および乗客数予測結果を示す。図2の緑線が評価データ(df_val)であり、赤線が予測確認データ(df_pred)である。評価データ、予測確認データの各360日分の内、タイムステップ幅に該当する128日分は予測値ではなく、その部分を予測するために与えた初期値であるのでオリジナルデータが使用されている(本来なら、その前の128日分を使用すべきである)。この結果より、まずまずの予測値が得られていると言える。
図1 LSTMモデルによる乗客数の機械学習の進行状況
図2 LSTMモデルによる乗客数予測結果
ARモデルによる未来予測結果
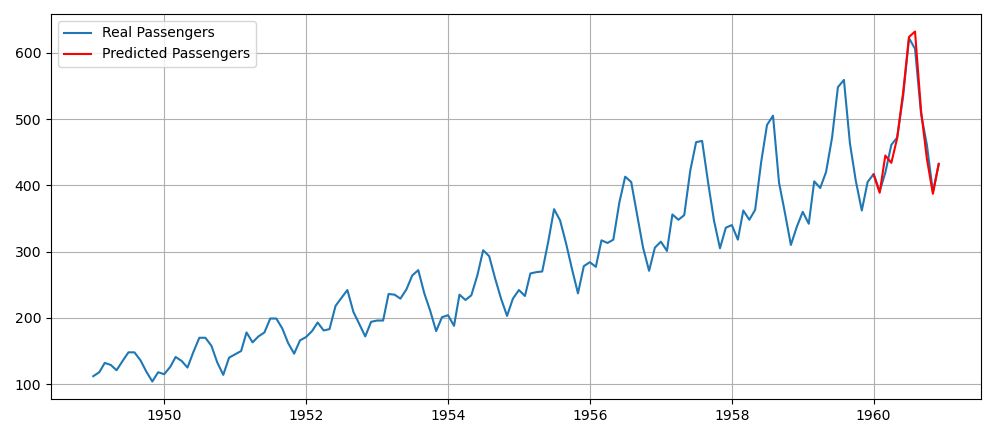
図3にオリジナルの月間データを使用したARモデルによる予測結果を示す。ARモデルの選定にはAIC(赤池情報量規準)を用いてパラメータ30項のモデルまで評価したが、結局パラメータ30項のモデルを使用した。1年間の旅客数の予測だけという目的であれば、ARモデルでも十分のようである。
図3 ARモデルによる予測結果
SARIMAモデルによる未来予測結果
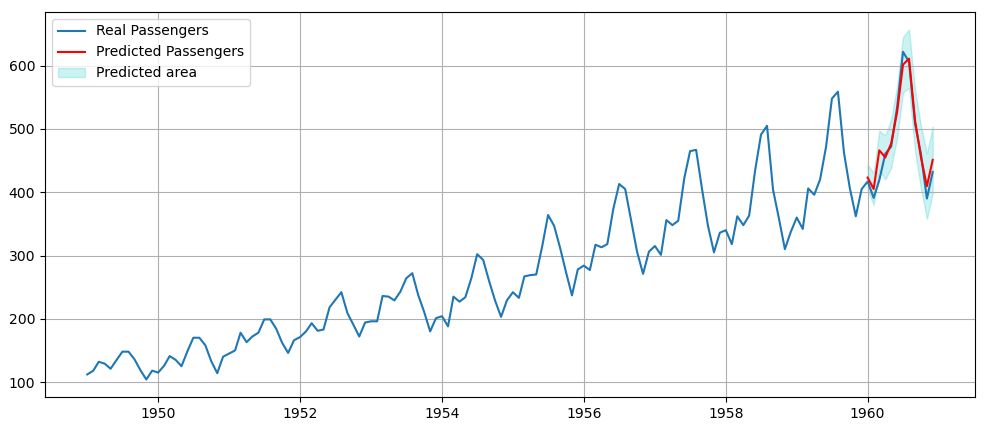
非季節性パラメータ\((p,d,q)=(3,0,1)\)、季節性パラメータ\((P, D, Q, m)=(0,1,0,12)\)を用いたSARIMAモデルを使用して12ヶ月先まで予測した結果を図4に示す。当然ではあるが、ARモデルと同様の良好な予測結果が得られている。
図4 SARIMAモデルによる12ヶ月間の予測結果
CNNモデルによる未来予測結果
上記AIモデルとしてLSTMモデルを使用したが、画像処理の分野でCNNモデルの精度の高さを体験した技術者として、単純な疑問が2つ芽生えている。第一の疑問は、時系列を考慮しない1次元CNNモデルでどの程度の精度で予測できるのか、という疑問である。第二の疑問は、時系列を考慮したLSTMモデルの代用としてCNNモデルで予測するとどの程度の精度で予測できるのか、という疑問である。
1次元CNNモデルによる未来予測結果
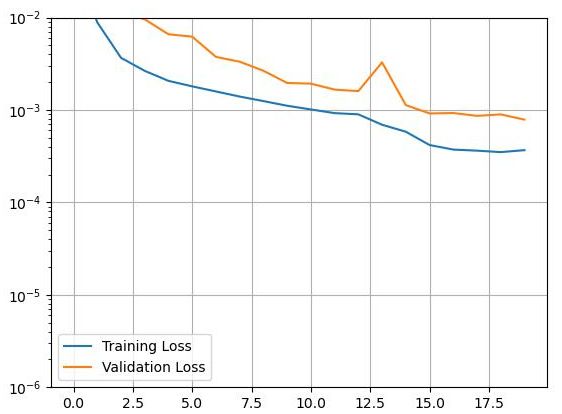
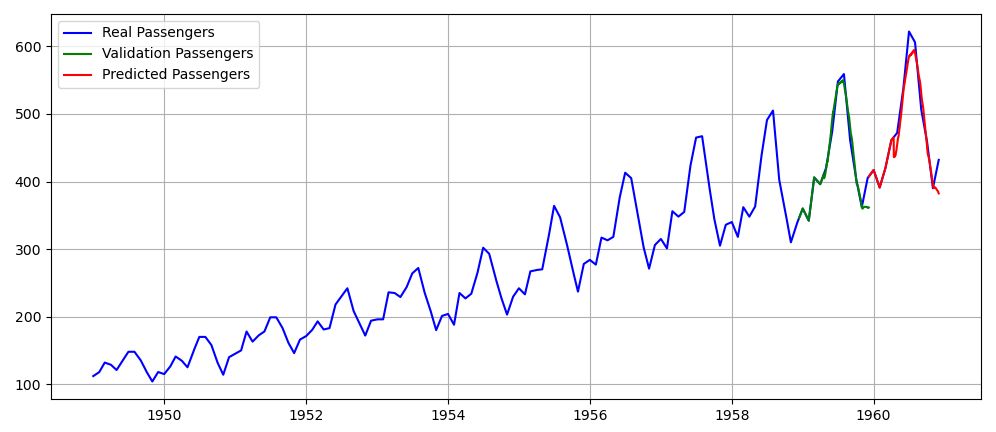
下図に示すような1次元CNNモデルを用いて、年月日を示す3列のデータのみから乗客数の予測を試みた。図5および図6に、1次元CNNモデルの機械学習の進行状況および乗客数予測結果を示す。この結果より、日付データのみからそこそこの予測は可能であるが、精度が不十分であると言える。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv1d (Conv1D) (None, 3, 16) 64
conv1d_1 (Conv1D) (None, 3, 32) 1568
conv1d_2 (Conv1D) (None, 3, 64) 6208
max_pooling1d (MaxPooling1D (None, 1, 64) 0
)
conv1d_3 (Conv1D) (None, 1, 128) 24704
flatten (Flatten) (None, 128) 0
dense (Dense) (None, 128) 16512
dense_1 (Dense) (None, 32) 4128
dense_2 (Dense) (None, 1) 33
=================================================================
Total params: 53,217
Trainable params: 53,217
Non-trainable params: 0
_________________________________________________________________
図5 1次元CNNモデルによる乗客数の機械学習の進行状況
図6 1次元CNNモデルによる乗客数予測結果
LSTMモデルの代用としてCNNモデルによる未来予測結果
上記LSTMモデルの代用として、下図に示すようなCNNモデルと時系列データから生成されたテンソルを用いて乗客数の予測を試みた。図5および図6に、CNNモデルの機械学習の進行状況および乗客数予測結果を示す。この結果より、LSTMモデルの代用にならなくはないけれども、やはりLSTMモデルに比較すると精度は劣ると言える。ただし、今回は、日付データの3列のみからの予測であったが、多要素を考慮しなければならないより複雑な課題においては、CNNが威力を発揮することがあるかも知れない。
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 128, 4, 16) 160
conv2d_1 (Conv2D) (None, 128, 4, 32) 4640
conv2d_2 (Conv2D) (None, 128, 4, 64) 18496
max_pooling2d (MaxPooling2D (None, 64, 2, 64) 0
)
conv2d_3 (Conv2D) (None, 64, 2, 64) 36928
conv2d_4 (Conv2D) (None, 64, 2, 64) 36928
max_pooling2d_1 (MaxPooling (None, 32, 1, 64) 0
2D)
conv2d_5 (Conv2D) (None, 32, 1, 64) 36928
conv2d_6 (Conv2D) (None, 32, 1, 64) 36928
flatten (Flatten) (None, 2048) 0
dense (Dense) (None, 128) 262272
dense_1 (Dense) (None, 32) 4128
dense_2 (Dense) (None, 1) 33
=================================================================
Total params: 437,441
Trainable params: 437,441
Non-trainable params: 0
_________________________________________________________________
図7 CNNモデルによる乗客数の機械学習の進行状況
図8 CNNモデルによる乗客数予測結果


-172.31.37.45。