時系列データの異常検知 - マロッタバルブの異常検知

AIゆめ
時系列データの異常検知は、心電図から異常を検知したり、製造業におけるサンプリングデータから異常を検知したりする目的などに活用できるでしょう。本ページで示すように日々AI技術を磨いていますので、製造業・非製造業に拘わらず、「自社の問題解決に応用できるのではないか?」と思われた方は、
ネオラクス・メール送信フォームからお気軽にご相談ください。AI技術を用いて、世の中にある様々な問題の解決に貢献して行きたいと思います。
時系列データの異常検知 - Autoencoderモデル
Autoencoderモデルは図1に示すように、encoderを用いて時系列データの次元を下げて特長量を抽出し、decoderで元の時系列データの次元に戻す。encoderは、tensorflow/kerasのConv1D、MaxPooling1D、Conv1Dの3層で構成され、decoderは、Conv1DTranspose、UpSampling1D、Conv1DTransposeの3層、そして元の時系列データに戻すConv1DTransposeで構成される。
画像セグメンテーションの分野ではencoder-decoderモデルとしてU-Netが良く知られているが、ここに示すオートエンコーダは、encoder-decoderモデルの1次元バージョンと考えて良い。Conv1D(1D畳み込み層)やMaxPooling1D(1Dマックスプーリング層)は、CNNモデルを扱った方であればイメージしやすいであろうが、Conv1DTranspose(1D転置畳み込み層)やUpSampling1D(1Dアップサンプリング層)は、馴染みがない方も多いかと思うが、Conv1DやMaxPooling1Dの逆操作と考えて頂ければ良い。
Autoencoderモデルでは、\(N\)個の元の時系列データから、\([[x_0,x_1,...x_{T-1}],[x_1,x_2,...x_{T}],...,[x_{N-T},x_{N-T+1},...x_{N}]]\)という\((N-T+1,T)\)個のデータを作成する。実際は、画像解析の分野でお馴染みのチャンネル数(カラーなら3、モノクロなら1)が加わるので、\((N-T+1,T,1)\)のテンソルを処理することになる。ここで、\(T\)は離散化した時間ステップ数であり、本ページでは\(T=64,128,256\)の3種類で比較する。図2に、Autoencoderモデルの各ステップにおけるテンソルのサイズを示す(\(T=128\)のケース)。
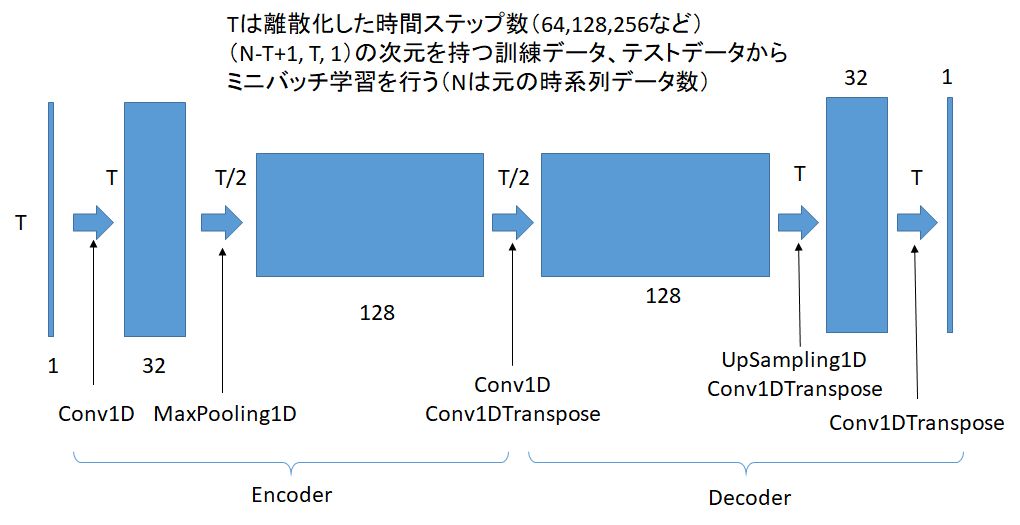
図1 Autoencoderモデル概要
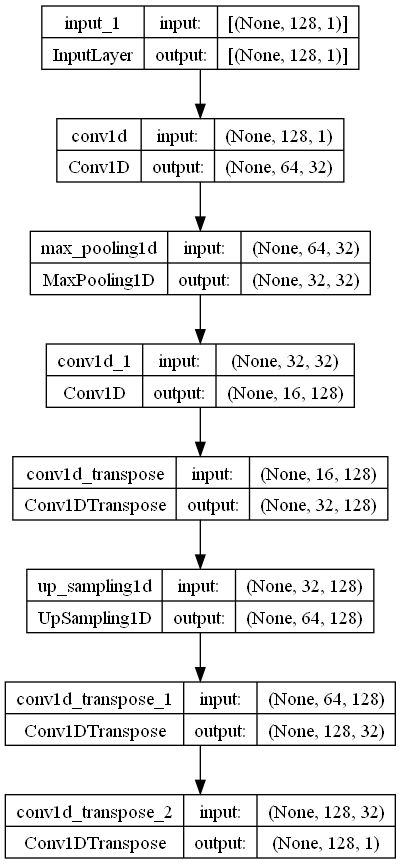
図2 Autoencoderモデルのテンソルのサイズ
(T=128のケース)
時系列データの異常検知 - 異常を検知するデータ
図3に、
公開データのTEK16.txtとTEK17.txtのデータから異常値を除去した波形を示す。図中の赤丸部分は、エンジニアが異常値であると指摘した箇所である。TEK16.txtの0~4000の範囲を訓練データとし、TEK17.txtの2000~3000の範囲を除く4000データをテストデータとして、機械学習を進めて、評価を行う。
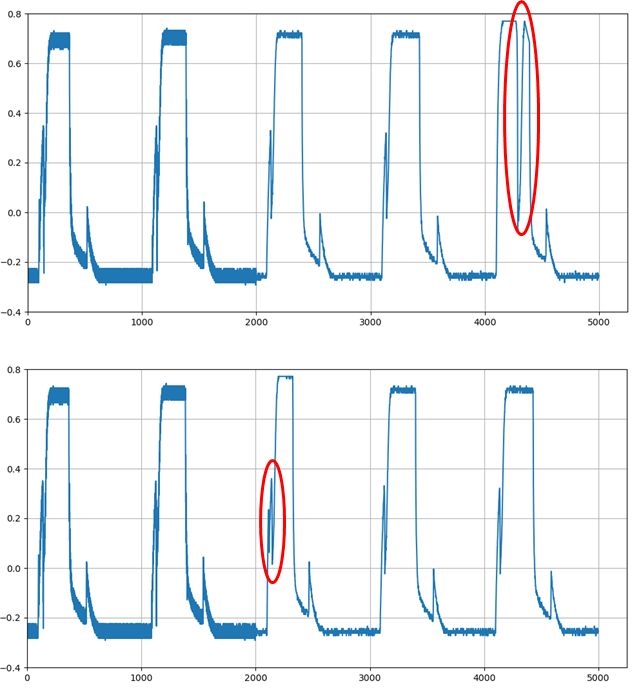
図3 マロッタバルブの波形(上:TEK16.txt, 下:TEK17.txt: 赤丸は異常が指摘されている箇所)
時系列データの異常検知 - 機械学習の状況
\(T=64,128,256\)の3種類のケースにおける機械学習の状況を図4~図6に示す。画像セグメンテーションにおけるU-Netや、チャットボットにおけるAttentionモデルの経験を基に、Autoencoderモデルの層の選択、層の深さ、フィルターサイズ(kerasのカーネルサイズ)などを調整した結果、図1、図2に示すモデルに落ち着いた訳である。特筆すべき点は、フィルターサイズと層の深さである。今回のデータは、1サイクル1000データの波形であり、学習データは4サイクルのデータしかない。このためフィルターサイズは28と、通常設定する値3~14よりかなり大きくした方が安定した学習結果が得られた。また、これ以上層を深くしても必ずしも良い結果は得られなかった。今回のモデルでは、どのケースも過学習は起こっておらず、まだ学習させることはできるが、この程度のロスであれば、ある程度納得できる結果が得られることが経験的にわかっているため、これ以上の学習は行わなかった。
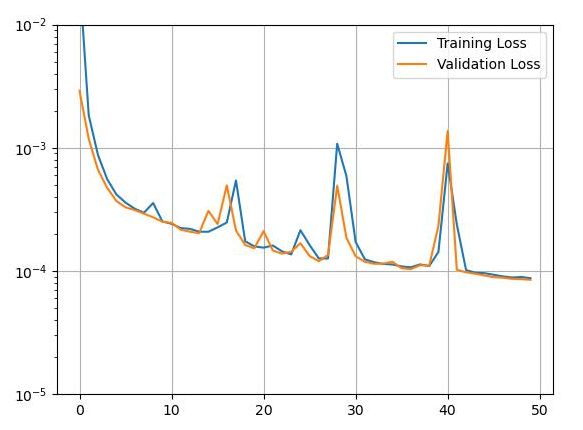
図4 機械学習の進行状況(T=64のケース)
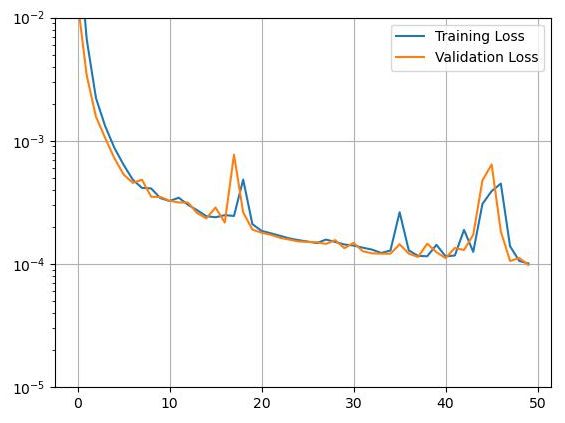
図5 機械学習の進行状況(T=128のケース)
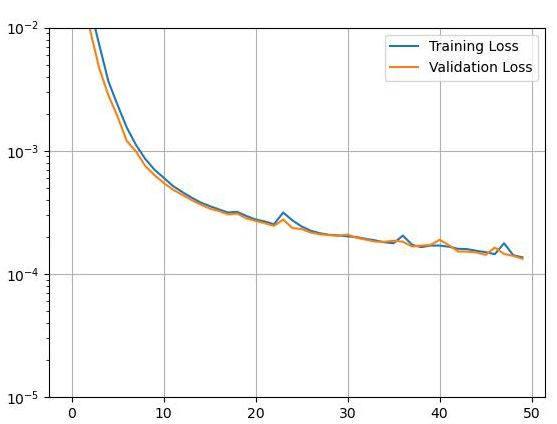
図6 機械学習の進行状況(T=256のケース)
時系列データの異常検知 - TEK16の異常検知
TEK16の異常検知 - 平均絶対誤差のヒストグラム
\(T=64,128,256\)の3種類のケースにおける学習データと異常を含む評価データについて、予測値との平均絶対誤差(MAE:Mean Absolute Error)のヒストグラムの比較を図7~図9に示す。学習データの予測値とのMAEに比較して、評価データの予測値とのMAEの差が大きいほど、異常を顕著に把握することができていることを意味している。即ち、図の赤丸の部分のヒストグラムの値が大きいほど、異常を顕著に把握することができているので、Tが大きいほど異常を顕著に把握することができていると言える。
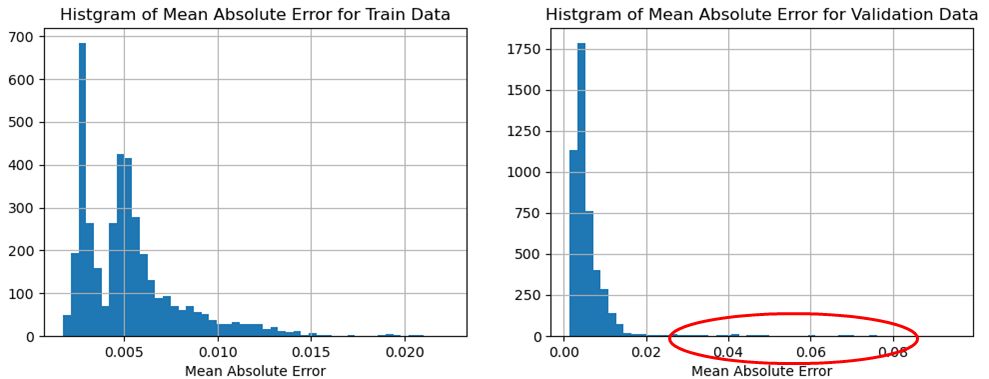
図7 学習データのMAE(左)とTEK16評価データのMAE(右)との比較(T=64のケース)
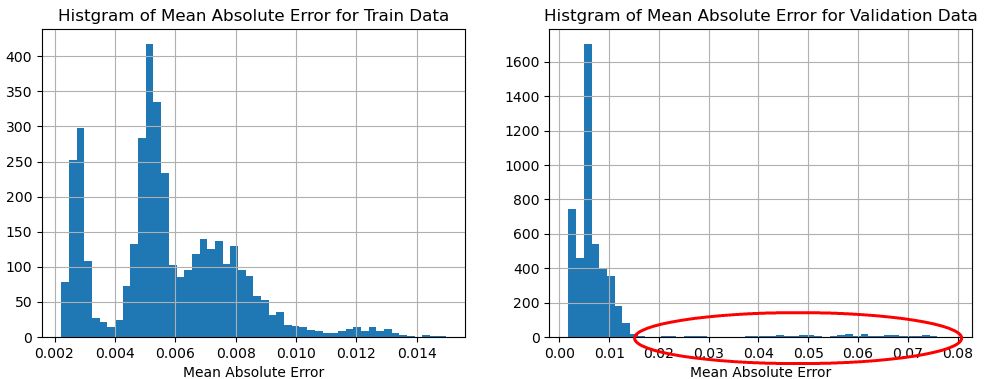
図8 学習データのMAE(左)とTEK16評価データのMAE(右)との比較(T=128のケース)
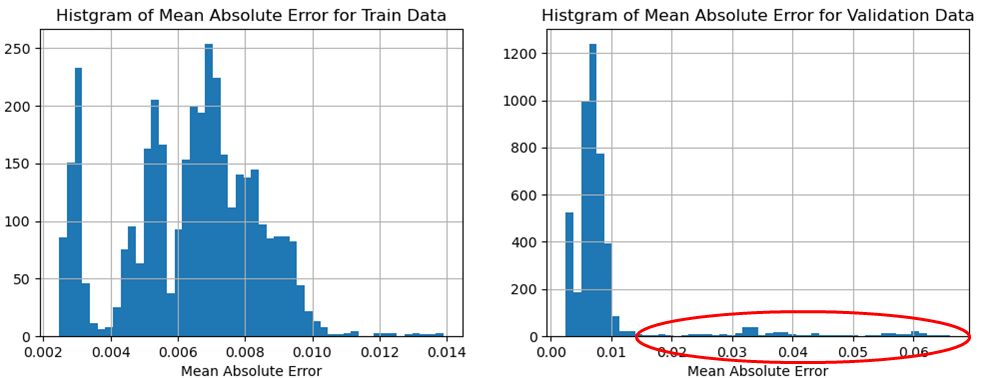
図9 学習データのMAE(左)とTEK16評価データのMAE(右)との比較(T=256のケース)
TEK16の異常検知 - 異常波形の予測
図10~図12は、\(T=64,128,256\)の3種類のケースにおける異常を含むTEK16の評価データ波形について、学習データのMAE上限閾値を超える部分を赤塗りでマークしたグラフである。
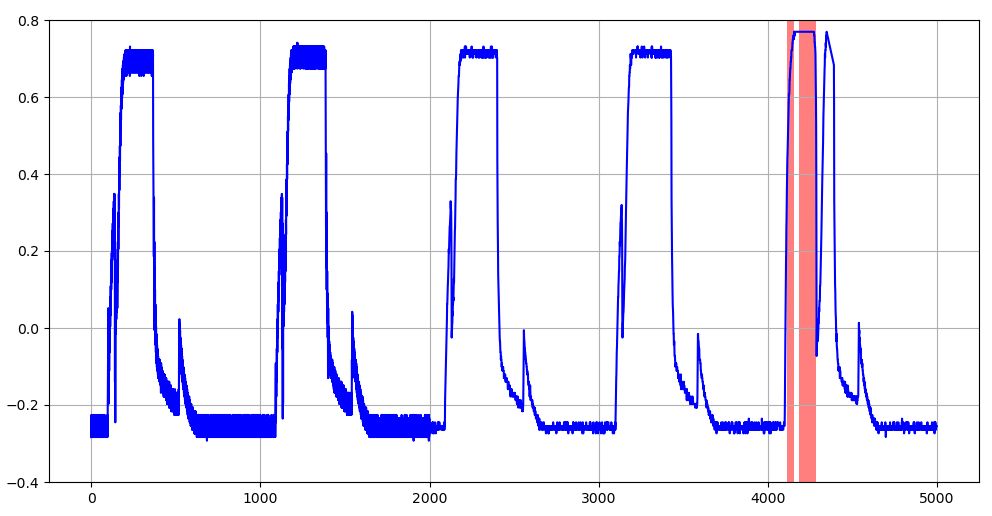
図10 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=64のケース)
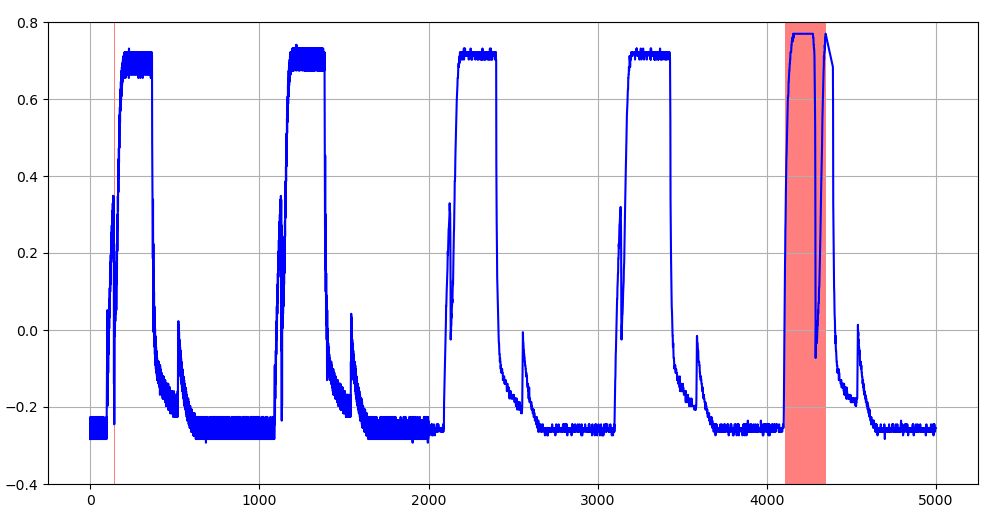
図11 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=128のケース)
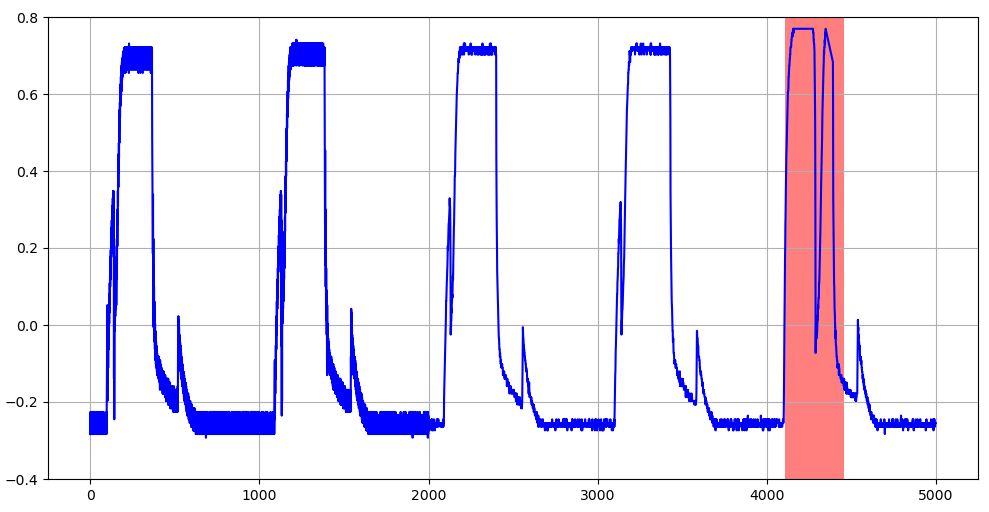
図12 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=256のケース)
時系列データの異常検知 - TEK17の異常検知
TEK17の異常検知 - 平均絶対誤差のヒストグラム
図13~図15のTEK17に関する平均絶対誤差のヒストグラムを見ると、全体的にTEK16よりも異常を顕著に把握することができていそうである。
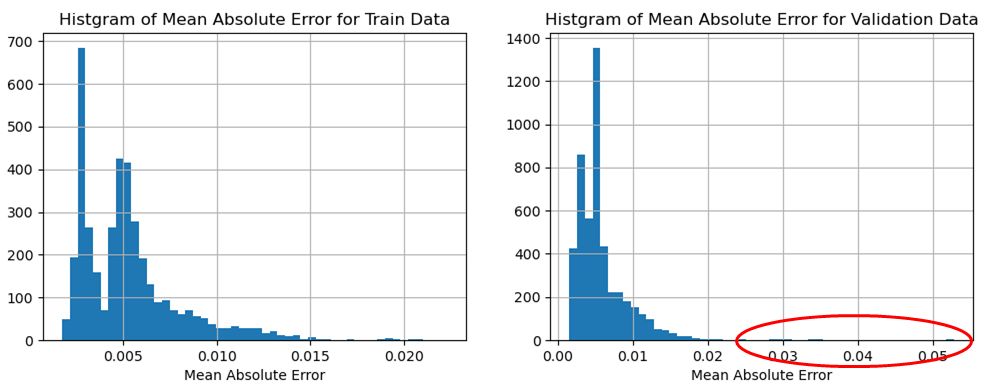
図13 学習データのMAE(左)とTEK17評価データのMAE(右)との比較(T=64のケース)
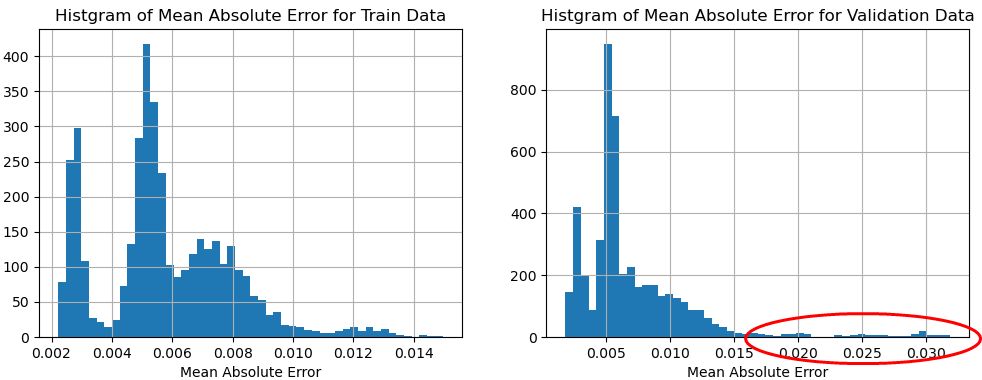
図14 学習データのMAE(左)とTEK17評価データのMAE(右)との比較(T=128のケース)
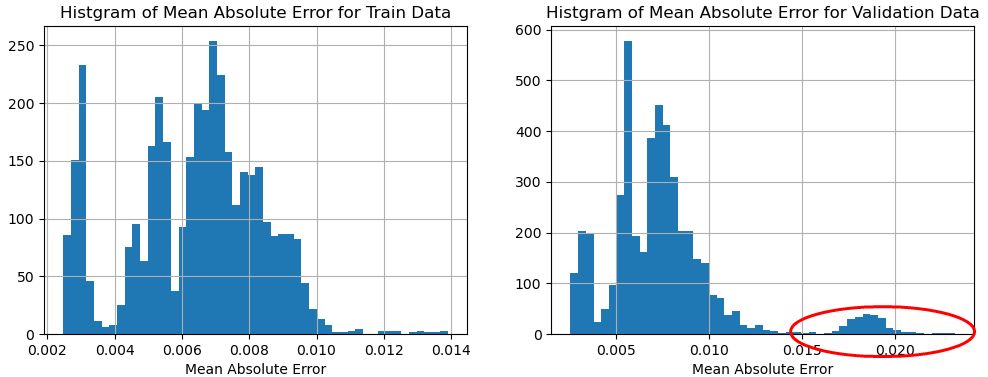
図15 学習データのMAE(左)とTEK17評価データのMAE(右)との比較(T=256のケース)
TEK17の異常検知 - 異常波形の予測
図16~図18は、\(T=64,128,256\)の3種類のケースにおける異常を含むTEK17の評価データ波形について、学習データのMAE上限閾値を超える部分を赤塗りでマークしたグラフである。\(T=64\)のケースでは、局所的な異常が的確に捕らえられ、\(T=256\)のケースでは、広範囲の異常として捉えられているようである。
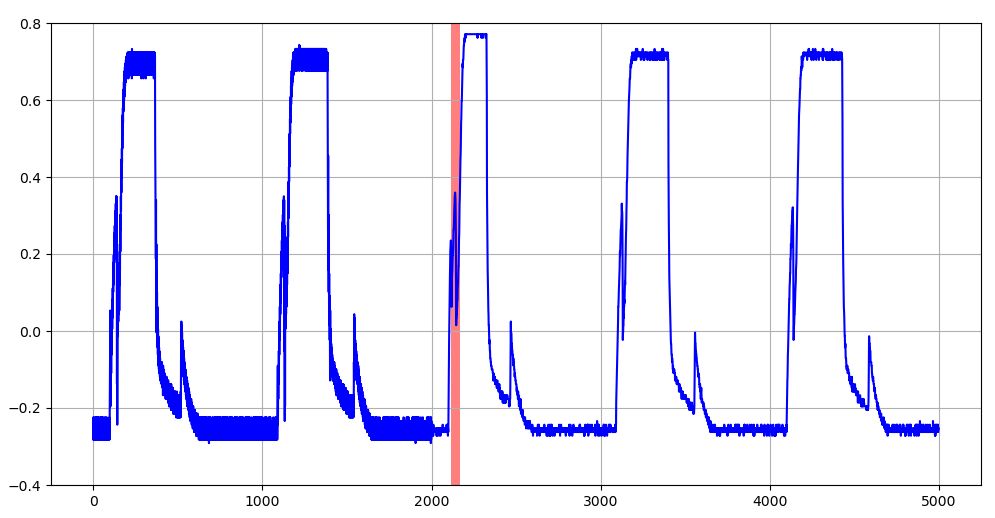
図16 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=64のケース)
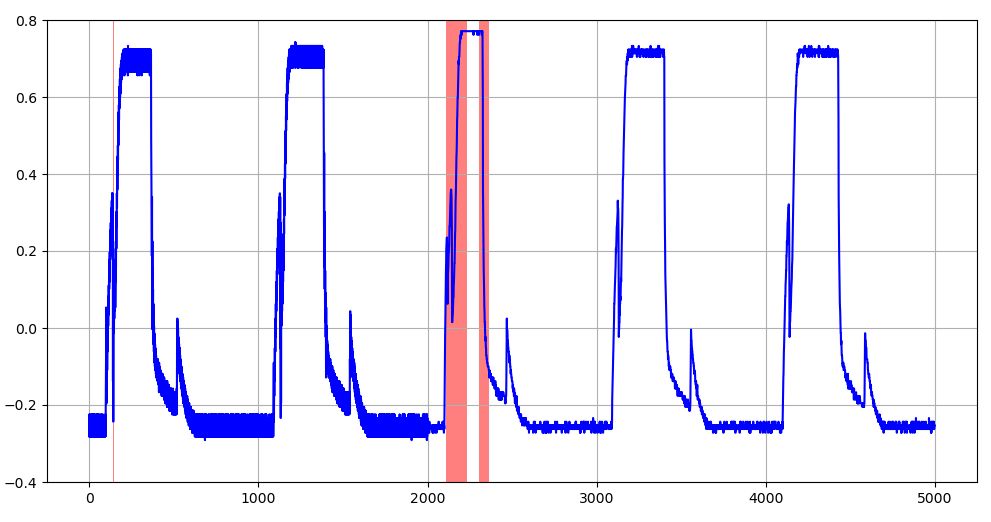
図17 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=128のケース)
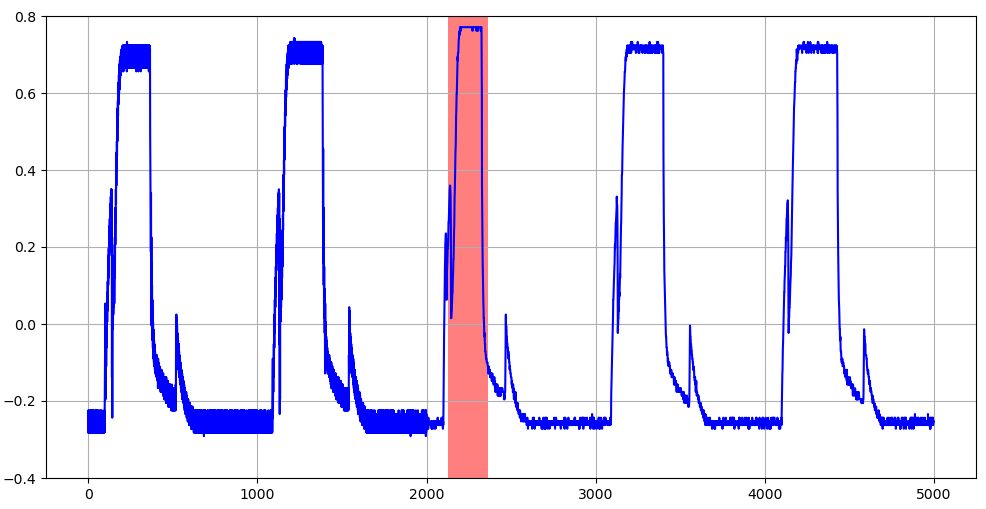
図18 学習データのMAE上限閾値を超える異常値を示す評価データ波形(赤塗りの部分:T=256のケース)
TEK17の異常検知 - 局所的な異常
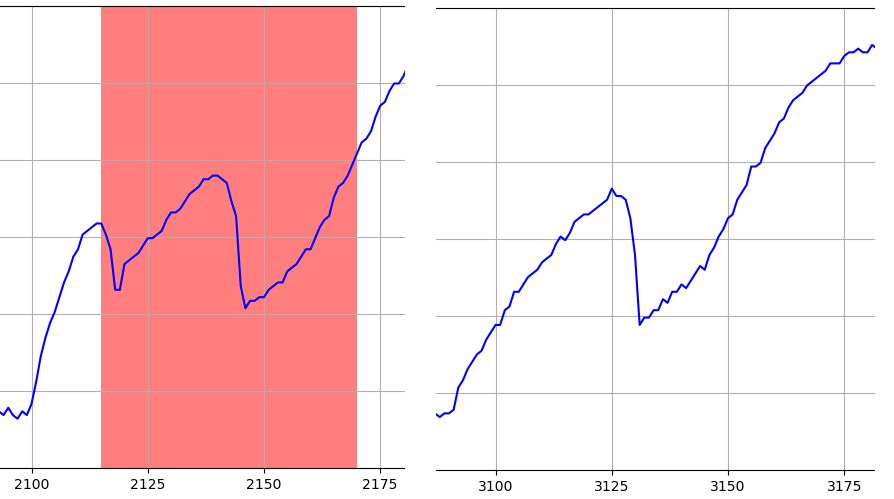
図19 TEK17の局所的な異常検知(T=64のケース:左が異常波形、右が正常波形)





















-172.31.37.45。