姿勢推定とは画像や動画から、人物の鼻、目、耳をはじめ肩、ひじ、手首、腰、ひざ、足首など17箇所のキーポイントを推定することにより、どんなポーズを取っているかを推定するAIです。特に、動画の姿勢推定を行えば、キーポイントの座標の変化がわかりますので、歩く姿勢、走る姿勢、ダンスのテクニックなど、理想とする人のデータを教師データとすることにより、被写体の習得レベルや課題がわかりやすくなるでしょう。

動画の時系列情報から運動の良し悪しを推定するAIモデルを作成するためには、本ページに示すような様々な統計処理を行って、どの部分が教師データと異なるかを調べ、慎重にモデル化を進める必要があります。製造業・非製造業に拘わらず、姿勢推定の応用例をご覧になって、「自社の問題解決に応用できるのではないか？」と思われた方は、ネオラクス・メール送信フォームからお気軽にご相談ください。AI技術を用いて、世の中にある様々な問題の解決に貢献して行きたいと思います。

詳しい説明はTensorFlowの姿勢推定やTensorFlow Hubに譲りますが、基本的にはCNN（畳み込みニューラル ネットワークモデル）で構成され、最大6人の姿勢を同時に検出できるようになったシステムです。早速、その応用例を見てみましょう。

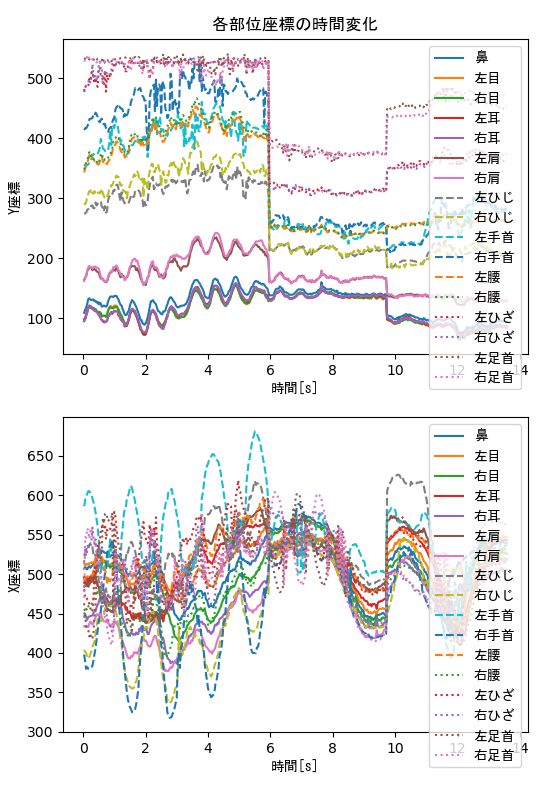
歩くモデルの姿勢推定サンプルとして、Pixabayの無料素材を利用させて頂きました。上の動画の通り、かなりうまく姿勢推定されているようです。この動画だけだと、なんとなく面白そうだけど、実際何に使うの？という疑問を持つ方も多いと思いますが、数の各キーポイントの画面上の座標の変化を抽出することができますので、このデータに周波数解析や統計解析を施すなどして、歩き方のモデルの入力変数として活用することができるでしょう。なお、この動画ではカメラも動いていますので、実際には使用することができません。また、画像や動画処理では左上が原点となり、下向きにY座標、横向きにX座標となっていますので、ご注意ください。

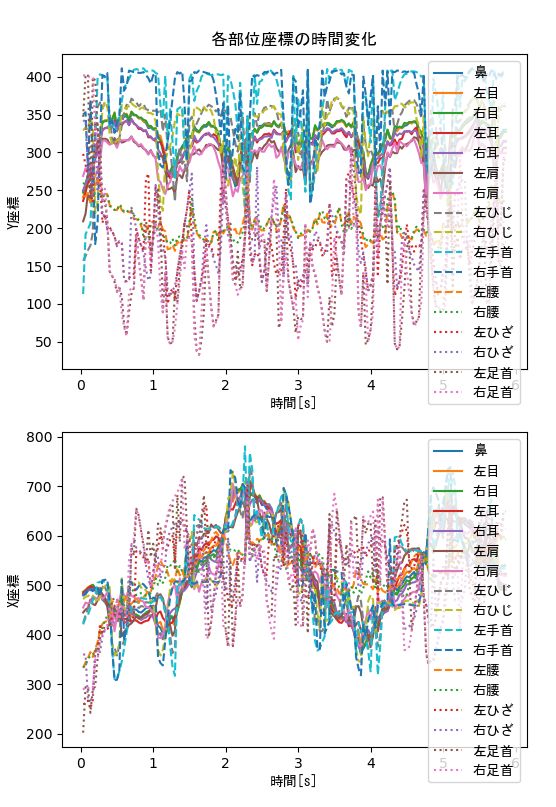
このモデルも上記サイトの無料素材を利用させて頂きました。動きが速いですが、うまく姿勢推定されているようです。

   ここでは、AIモデルの精度を決める特徴量をどのように選択して行くか、歩くモデルのデータを使ってその一例を示ししましょう。この、特徴量は、画像解析においては、画像の回転、スケール変化、照明の変化などに頑強なSIFT(Scale-Inrarient Feature:例えば画像の輝度変化の空間ベクトル)やHOG(Histogram of original gradient:指向性のある勾配ヒストグラム)であったり、自然言語処理においては、word2vecに用いられるような単語の近さを表す単語ベクトルであったりしますが、どちらもCNNやLSTMという学習手法の中で、画像や文章から自動的にフィルタリングして抽出されます。

しかし、一般的な問題においては、膨大な情報の中から、目的を達成するために効果的な特徴量を、様々な統計的解析手法を用いて選定する必要があります。上記の歩くモデルであれば、画像から歩き方の良し悪しを判定したり、健常者と障害者を見分けたりするモデルが考えられるでしょう。例えば、健常者と障害者を見分けるモデルであれば、両者の歩き方を撮影した多数の動画から得られる膨大な時系列データを用いて、歩き方の違いを端的に表す特徴量を探求する作業がモデル作成の第一ステップになります。この作業は、EDA（Explanatory Data Analysis：探索的データ解析）と呼ばれています。そして、動画だけではなく、音声モデルや製造現場での異常診断モデルなどにおいても、このEDA手法を用いて、時系列データからうまく特徴量を抽出する作業が、モデルの優劣を左右する最も重要な行程であると言えるでしょう。

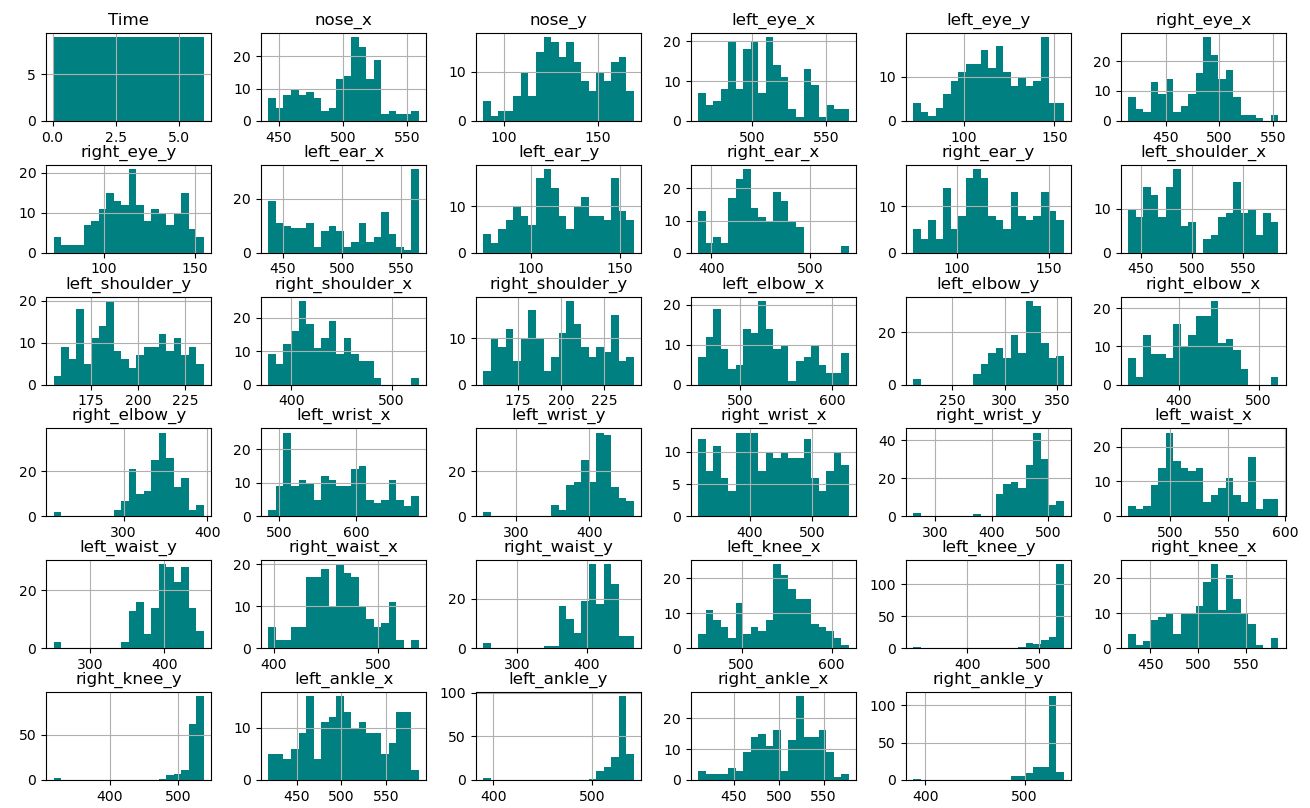
   上記の歩くモデルでは、動画の6秒付近でカメラが切り替わっていますので、切り替わる前のデータを利用します。切り替わる前にもカメラが動いていますが、実際の動画解析では、目的を達成するため動画撮影方法から慎重に検討する必要がありますが、ここでは、あくまで特徴量抽出例のデモンストレーションとしてご覧ください。下図は、各キーポイント座標のヒストグラム（各キーポイントがその座標（ピクセル値）に来る頻度）です。なお、描画に使用しているmatplotlibのpyplotは非常に便利なのですが、日本語が文字化けを起こし、その対応がWindowsとLinuxで異なるなど不便な点もあるので、各キーポイントの名称は英語表記に戻しています。

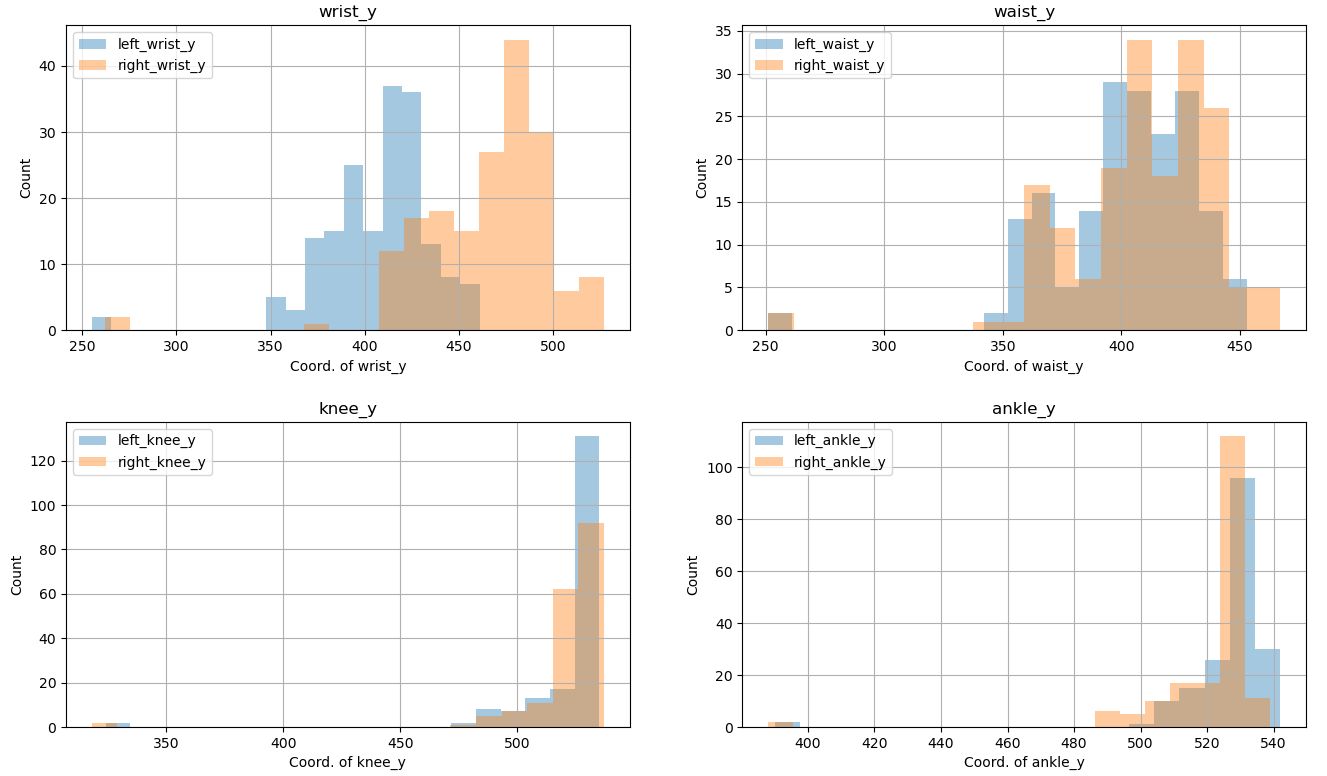
そして、全体のヒストグラムを見渡して、気になるヒストグラムがあれば重ね合わせることにより詳細に分析します。今回は、同じ人の画像データから抽出した動きを重ね合わせていますが、上述の健常者と障害者を見分けるモデルであれば、健常者と障害者のヒストグラムを重ね合わせるのが良いでしょう。

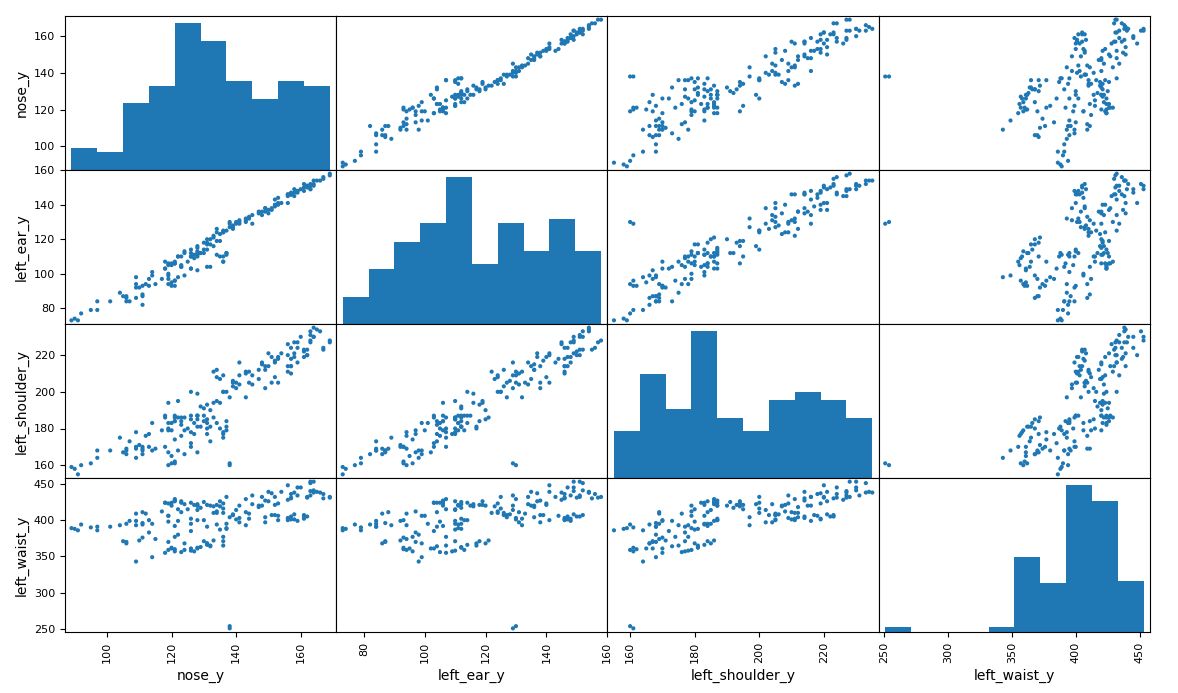
   2つの特徴量の相関関係も、モデルを構築する上で重要なヒントを与えてくれますので、散布図も積極的に活用します。下図の例であればnose_yとleft_ear_yはかなり相関が高いようですので、どちらかに搾り込むことができるでしょう。

   関数\(f(t)\)を周波数\(ω\)の正弦波に分解して関数\(F(ω)\)を求める演算がフーリエ変換であり、計測時刻\(t_{n}\)における計測値\(f_{n}\)を離散的な周波数\(ω_{k}\)の正弦波に分解して関数\(F(ω_{k})　k=0,1,2,...,N-1\)を求める演算が離散フーリエ変換です。そして、これを高速に演算するのが高速フーリエ変換(FFT)であり、Nが2の冪乗でなければなりません。

numpyを使用すれば、Nが2の冪乗でなくてもこのFFTを簡単に計算できます（多分2の冪乗を超えたデータを0にしている）が、低周波の部分が重要である場合には、やはりNが2の冪乗であるというルールを守った方がよさそうです。また、アナログ信号をデジタル信号に正確に変換する際の注意点は、サンプリング周波数の1/2以下の周波数が有効であるという標本化定理（サンプリング定理）があることです。一般の動画は、1秒間に30フレーム（30Hz）ですから、有効であるのは15Hz以下となります。

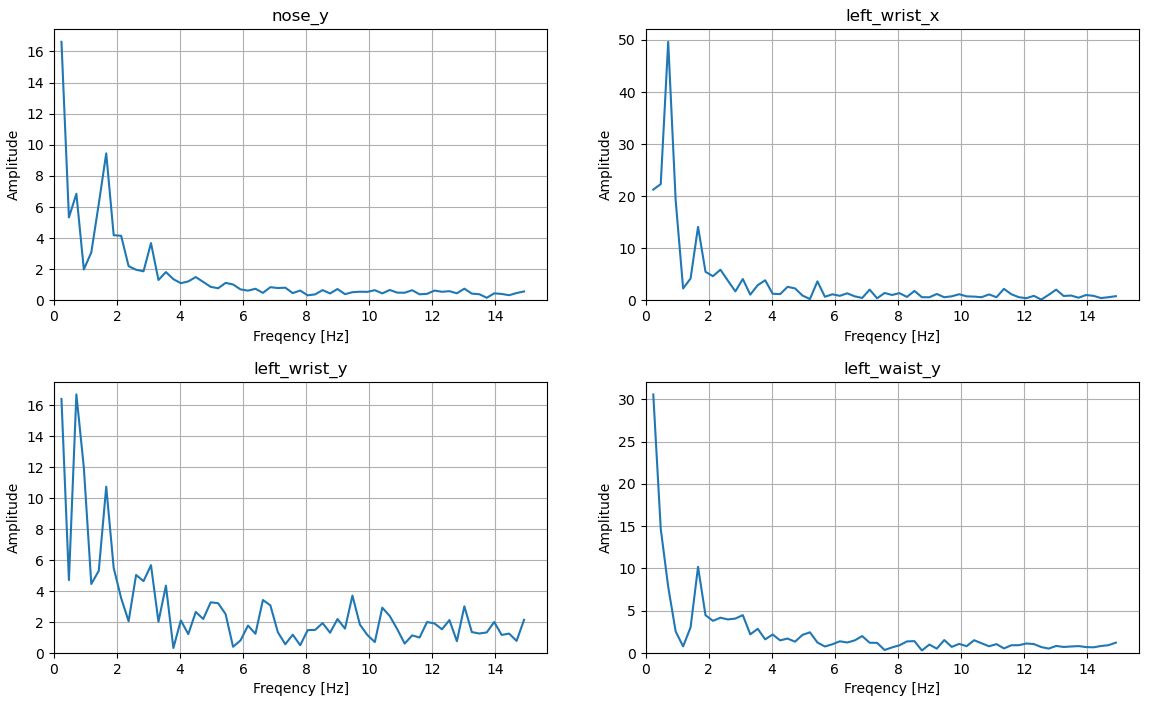
下図は、4か所のキーポイント座標のFFTの結果です。Nが2の冪乗という制約からN=128（動画の4.2秒迄）としました。勢いよく手を振って歩いていますので、左手x座標(left_wrist_x)が1往復する2歩の周波数(0.8Hz付近)に強いピークが現れ、一歩の周波数（1.6Hz付近）に次のピークが現れています。このようにFFTの処理結果も、場合によっては重要な特長量となるケースがあります。例えば、機械の故障前には稼働音の高周波成分の強度が増えることがあります。熟練者であれば、古くなった機械の異常音から「何かおかしい」と異常検出できるでしょう。機械の音のFFT結果を入力として機械学習すれば、機械の異常検出モデルの精度が向上する可能性が高いでしょう。

   周期性の強い時系列データの変化による異常判断モデルなど、周期性の強い時系列データを扱う場合にはARモデル（自己回帰モデル）の係数の変化、自己相関関数の変化などが有用な情報を与えてくれることがあります。時刻\(t\)における変数\(y_t\)は、ARモデルでは以下のように表現されます。 \begin{align} y_t = \sum_{ i = 1 }^{ P } φ_i y_{t-i} + ε_t + c \tag{1} \end{align} ここで、\(φ_i\)はARパラメーター、\(ε_t\)は白色雑音（ホワイトノイズ）、\(c\)は定数です。即ちこのモデルは、時刻\(t\)における変数\(y_{t}\)が、現在より\(i\)時刻前の過去の自分の値、ホワイトノイズ、定数の合計で示されるというモデルです（\(i=1,2,3,...,P\)）。

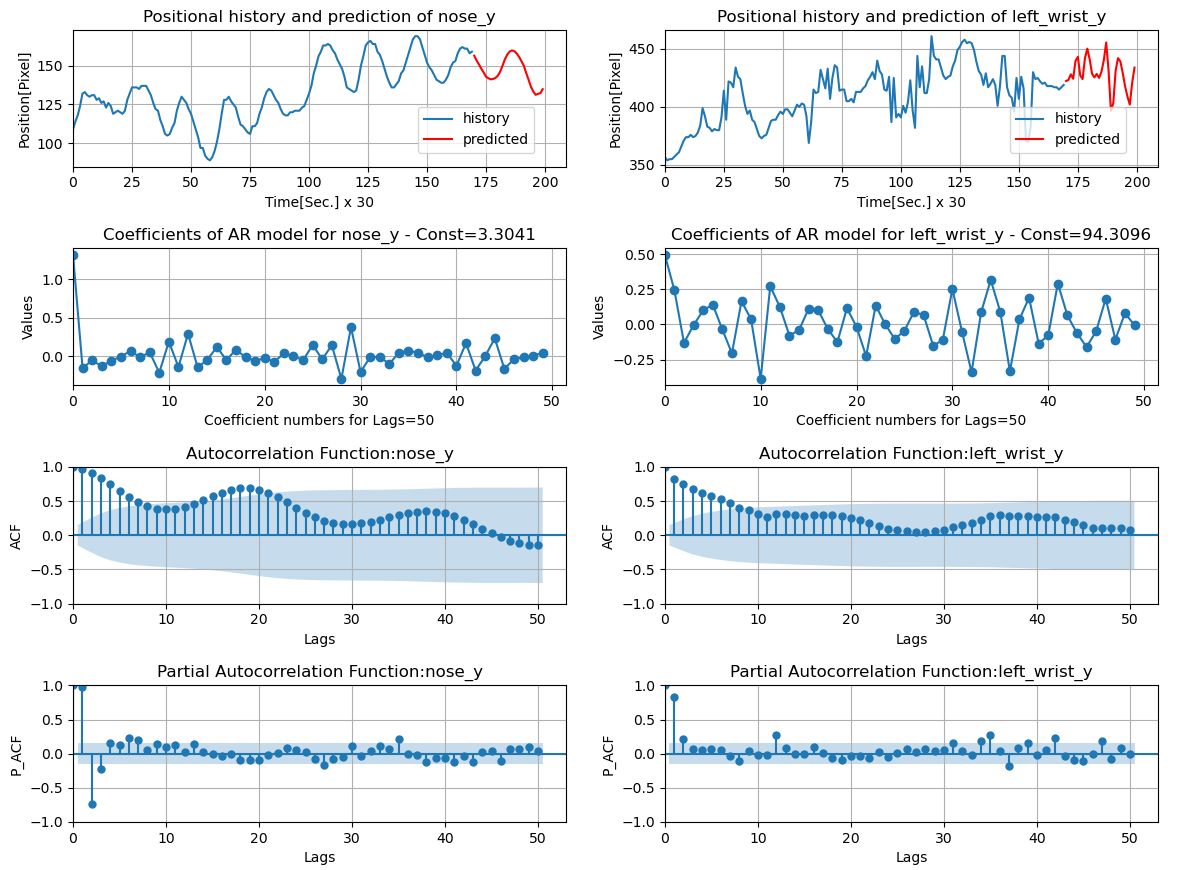
そして、このモデルをnose_yとleft_wrist_yに適用した結果は下図のようになります。最上段が時間による座標の変化（赤線は1秒後までの予測値：描画の都合上横軸が秒数の30倍になっていることに注意）、2段目が各ARパラメーター\(φ_i\)、3段目が自己相関関数（autocorrelation function）、4段目が偏自己相関関数（partial autocorrelation function）です。ここで、変数\(y_{t}\)と変数\(y_{t-i}\)の関係性の強さは、時差\(i\)の自己共分散で表現されますが、この自己共分散を0～1の数値で正規化したものが時差\(i\)の自己相関です。そして、自己相関は\(i=1,2,3,...,P\)の間で分布しますので、これを自己相関関数と呼びます。なお、自己相関関数と偏自己相関関数のグラフで青い網掛けの部分は、自己相関がゼロである確率が95%である範囲（95%信頼区間:95 % confidence intervalsと呼ぶ）を示しています。即ち、この範囲の外側にあれば、ほぼ間違いなく相関があると考えれば良いでしょう。

さて、あまり聞きなれない偏自己相関関数の説明ですが、仮に、変数\(y_t\)が、次式のように\(t-1\)時刻の変数\(y_{t-1}\)のみと関係があると仮定しましょう。 \begin{align} y_t = φ_1 y_{t-1} \tag{2} \end{align} この場合、変数\(y_t\)と変数\(y_{t-2}\)は、関係がないように見えますので、この2変数の共分散（自己相関）は0になることが期待されます。しかし、(2)式を\(t-2\)時刻まで展開すると、 \begin{align} y_t = φ_1 φ_2 y_{t-2} \tag{3} \end{align} という関係を導くことができますので、期待に反して、変数\(y_t\)と変数\(y_{t-2}\)の共分散は0にはなりません。そして、変数\(y_t\)と変数\(y_{t-2}\)の自己相関を求める際に、変数\(y_t\)と変数\(y_{t-1}\)の自己相関の影響を取り除いたものが偏自己相関です。したがって、偏自己相関関数はより真実に近い自己相関を示しており、(1)式で表現されるARパラメーターにより近いと考えて良いでしょう。なお、今回使用したデータは、それ程周期性が強くないため、これらの統計情報はあまり活用できないかも知れませんが、あくまで一般論として記述させて頂きました。

   自己相関関数は上述の通り、時差\(i\)の自己共分散、即ち、時間をずらした時の自分自身の類似性であることを述べましたが、時系列データを扱う場合には、自己相関関数と並んで重要な要素が相互相関関数（cross-correlation function）です。相互相関関数とは、時差\(i\)の自己共分散、即ち、時間をずらした時の二つの信号の類似性を0～1の数値で正規化したものです。運動の上手さや歩き方の美しさなどを判断する基準としては、各部位の相互相関関数が重要な働きをするでしょう。ここでは、上記、ブレークダンスモデルのデータを使用して、各部位の相互相関関数を見てみましょう。

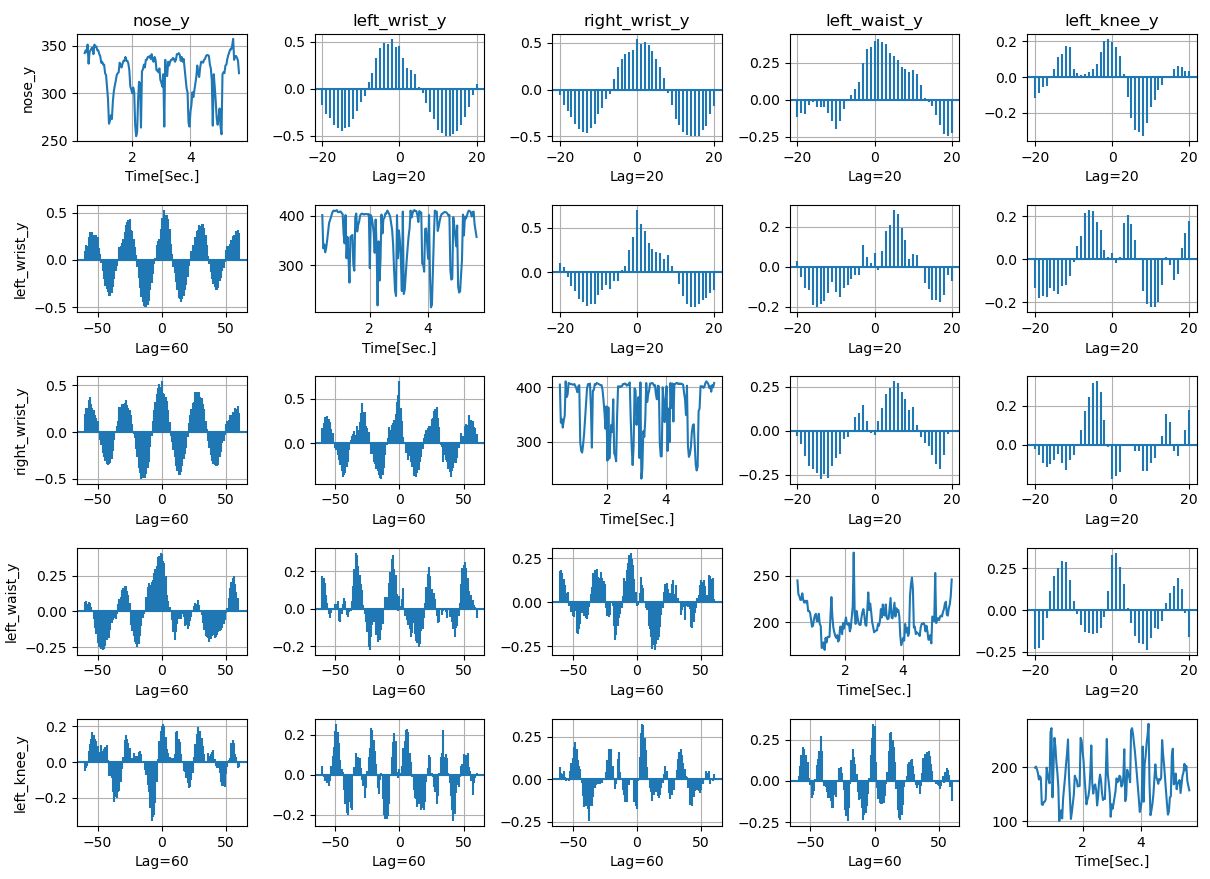
下図では、対角線上に解析したその信号の波形（定常運動に入る初期の部分は削除）、その右上にLag=20フレーム(0.66秒)の相互相関関数、左下にLag=60フレームの相互相関関数を示しています。それぞれ、行の左に記述されている部位に対する、列の上に記述されている部位の相互相関関数を表示しています。例えば、上段の左から２番目と３番目を比較すれば、'nose_y'に比較して'left_wrist_y'がわずかに進み、'right_wrist_y'がわずかに遅れていることがわかります。このような情報を、ブレークダンス上手な人と下手な人の情報として整理し、ブレークダンスモデルの入力データとして学習させれば、良いAIモデルとなることでしょう。