時系列情報が学習できるRNN概要

AIゆめ
このような弱点を克服したのがRNN(Recurrent Neural Network:再帰ニューラルネットワーク)ですが、RNNは長い文章の学習において、
勾配消失や勾配爆発が発生するという課題を抱えていました。
そして、このような課題を解決したのがRNNの発展系であるLSTM(Long Short-Term Memory:長期の短期記憶を備えたニューラルネットワーク)や
GRU(Gated Recurrent Unit:ゲート付き再帰ユニットによるニューラルネットワーク)などゲート付きRNNと呼ばれるニューラルネットワークです。
さらに、Encoder-Decoderモデルと呼ばれるseq2seq(Sequence to Sequence)技術においてAttentionという強力な技術が開発されて学習時間が大幅に短縮されることにより、
チャットや翻訳などの自然言語処理の分野でニューラルネットワークへの応用が一気に加速されて来た感があります。
AIゆめの夢占いチャットもLSTMやAttentionという技術が無ければ開設することができなかったでしょう。
また、最近の研究では、RNNの
活性化関数を変更することにより、
LSTMと同等以上の性能を持つRNNの研究が行われるなど、この分野の技術の進歩には目を見張るものがありますので、しばらくはニューラルネットワークの最新の研究から目を離せないでしょう。
時系列情報が学習できるRNNの目次
時系列情報が学習できるRNNの理論
RNNの基本概念
RNNでは入出力層、隠れ層共に時刻情報を持った時系列情報として扱い、離散化した時刻\(t\)における入出力層や隠れ層の状態に添え字\(t\)を付加して\(h_{tj}^{(L)}\)のように表現します。
各時刻における各層の状態は、
ニューラルネットワークの数式表現
の項で説明した通り行ベクトルですが、全時刻をまとめた\(h_{tj}^{(L)}\)は行列になります。
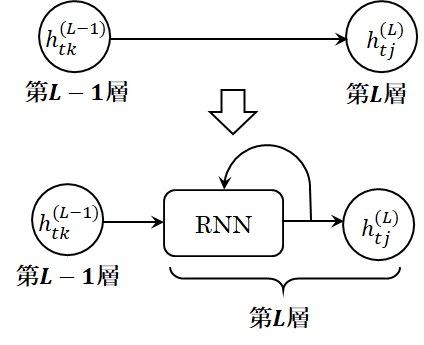
図1 FF型ニューラルネットワークとRNN
しかし、時系列データが多くなって行くに従い図1に示すRNNは図2に示す展開したRNNに近づいて行くことがわかります。
ここで、\((h_{j}^{(L)})_t\)は、行列\(h_{tj}^{(L)}\)の時刻\(t\)における行ベクトル要素であることを意味しています(\(t=0\) ~ \(T-1\))。
これは、微分方程式が離散化した差分方程式で表され、その時間刻みを無限に小さくして行くと両者が一致することから容易に類推できるでしょう。
そして、このように展開したRNNであれば、FF型ニューラルネットワークの類推から、容易に数式表現できることが理解できるでしょう。
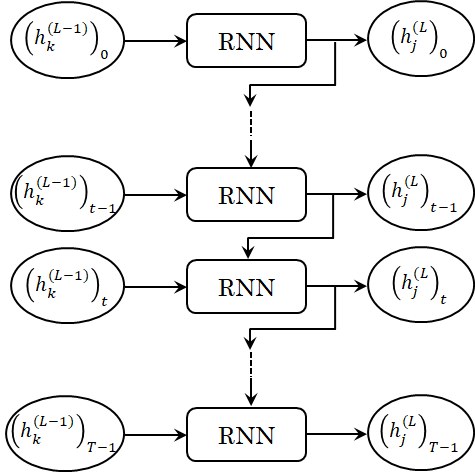
図2 展開したRNN
RNNの数式表現
図2に示す展開したRNNの情報の流れからRNNの数式表現を見てみましょう。
第\(L\)層の時刻\(t\)におけるRNNボックスへの入力は、\(h_{tj}^{(L-1)}\)と\(h_{t-1,j}^{(L)}\)になっています。
ここで、時刻\(t-1\)における行列\(h_{t-1,j}^{(L)}\)は、混乱を防ぐため添え字\(t-1\)と\(j\)との間に'\(,\)'を入れて読みやすくしていますが、
これは前記の要素表現のルールに従えば、行列要素を表す場合には\((h_{j}^{(L)})_{t-1}\)という表現になります。
そして、
FF(Feed Forward:フィードフォワード)型のニューラルネットワークの数式表現
と同様、重みとバイアスを使用して数式表現すれば次式のようになります。
\[
h_{tj}^{(L)} = \tanh(h_{t-1,i}^{(L)} w_{ij}^{(L)} + h_{tk}^{(L-1)} w_{kj}^{(L-1)} + b_{tj}^{(L)}) \tag{1}
\]
ここで、一般的に、第\(L\)層と第\(L-1\)層の隠れ層ではベクトルの次元数が異なりますので、\(h_{t-1,i}^{(L)}\)や\(h_{tk}^{(L-1)}\)のように、
アインシュタインの総和規約が適用される変数を\(i\),\(k\)とあえて異なる変数で表記しています。
そして、RNN層は
Embedding層の後に来ますので、
第\(L-1\)層の添え字の範囲は\(k=0~D-1\)となり、第\(L\)層の添え字の範囲は\(i=0~H-1\),\(j=0~H-1\)となります。
ここで、\(D\)は単語の意味表す単語ベクトルの次元数であり、\(H\)は出力側の隠れ層の状態ベクトルの次元数です。
また、第\(L\)層のバイアス\(b_{j}^{(L)}\)は時系列変数\(t\)には無関係なパラメータですが、(1)式では隠れ層の状態\(h_{tj}^{(L)}\)と次元を一致させるため\(b_{tj}^{(L)}\)と表記されています。
そして、\(t\)方向には毎回同じ重み\(w_{ij}^{(L)}\), \(w_{kj}^{(L-1)} \)やバイアス\(b_{j}^{(L)}\)が使用されることになります。
RNNの活性化関数として使用されているハイパボリック・タンジェント(hyperbolic tangent)関数\(\tanh(x)\)は出力を-1~1で正規化します。
\[
y = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} \tag{2}
\]
そして、このハイパボリック・タンジェント関数は、
その他の活性化関数
の項で示す通り、シグモイド関数と密接な関係があります。
RNNの実装 - バッチ処理
Encoder-Decoderモデルの学習の際にはEncoderへの入力データとDecoderの教師データの大量の組み合わせデータが使用されます。
このような大量のデータをコンピュータで処理する場合には、1データずつ処理するよりも大量のデータをまとめて処理する方が入出力が効率的になったり、
計算を並列化できたりして1データ当たりの処理時間が大幅に短縮されますので、大量のデータをまとめて処理するバッチ処理が行われます。
(1)式で表されるRNNの数式表現を、バッチ処理を考慮した数式で表現すると次式で示す通りベクトルや行列の次元が一次元づつ増えることになります。
ここで、\(n=0~N-1\)は、バッチサイズNのバッチに関する変数を意味しています。
\[
h_{ntj}^{(L)} = \tanh(A_{ntj}^{(L)}) \tag{3}
\]
\[
A_{ntj}^{(L)} = h_{n,t-1,i}^{(L)} w_{ij}^{(L)} + h_{ntk}^{(L-1)} w_{kj}^{(L-1)} + b_{ntj}^{(L)} \tag{4}
\]
そして、RNNの数式表現を図式で表現すると図3のようになります。この図では図2を90度回転させた向きの表記ですので、横軸が時刻\(t\)であり縦軸が層番号\(L\)であることに注意してください。
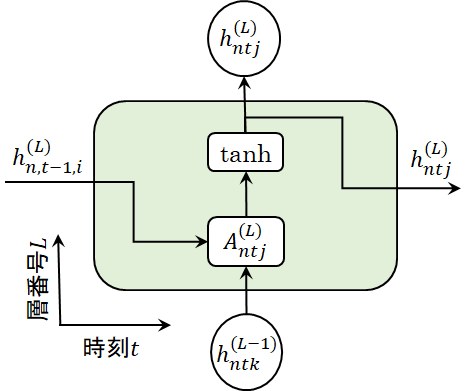
図3 RNN層の図式表現
RNN層の単一時刻における処理
バッチ処理を考慮した(3)式、(4)式を一気に解こうとすると処理が複雑になってしまいますので、バッチ処理の部分と時刻処理の部分を切り離して処理することを考えます。
まず、図3において、時刻\(t\)の要素を\(( )_t\)と表現すれば、RNN層の時刻\(t\)要素は(5)式あるいは図5のように表現できます。
\begin{align}
(h_{nj}^{(L)})_t &= \tanh( (h_{ni}^{(L)})_{t-1} w_{ij}^{(L)} + (h_{nk}^{(L-1)})_t w_{kj}^{(L-1)} + b_{nj}^{(L)} ) \nonumber \\
&= FW ( (h_{nk}^{(L-1)})_t, (h_{ni}^{(L)})_{t-1} ) \tag{5}
\end{align}
即ち、時刻\(t\)における\(h_{nk}^{(L-1)}\)と時刻\(t-1\)における\(h_{ni}^{(L)}\)という2つの行列変数を入力とし、
時刻\(t\)における\(h_{nj}^{(L)}\)という行列変数を出力とする関数\(FW()\)が定義でき、これが単一時刻\(t\)におけるRNN層の処理となります。
ここで、第\(L\)層のバイアス\(b_{j}^{(L)}\)はバッチ変数\(n\)には無関係なパラメータですが、(5)式では隠れ層の状態\((h_{nj}^{(L)})_t\)と次元を一致させるため\(b_{nj}^{(L)}\)と表記されています。
これは、\(n\)方向に値をコピーするというNumPyのブロードキャストという機能を使用してバイアス\(b_{j}^{(L)}\)が\(n\)方向にコピーされることになります。
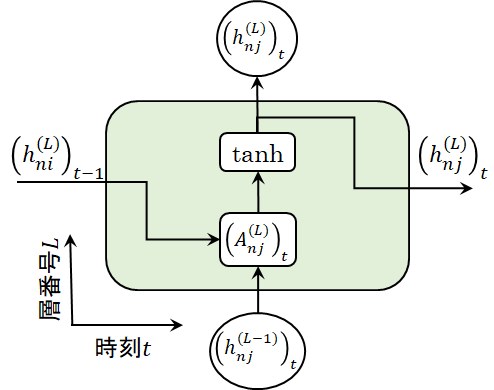
図4 RNN層の時刻\(t\)要素の図式表現
RNN層の時系列行列の設定
時刻\(t\)におけるRNN層の各要素の計算ができれば、後はこの要素を時系列行列として設定するだけですので、次式や図5に示す通り\((h_{nj}^{(L)})_t\)を\(h_{ntj}^{(L)}\)の要素として登録すれば完了です。
\[
h_{ntj}^{(L)} = \begin{pmatrix} (h_{nj}^{(L)})_0 & (h_{nj}^{(L)})_1 & ... & (h_{nj}^{(L)})_t & ... & (h_{nj}^{(L)})_T-1 \end{pmatrix} \tag{6}
\]
なお、RNN層を実装するためにはRNN層の誤差逆伝播も数式表現する必要があります。
RNN層の誤差逆伝播の詳細は、
RNN層の誤差逆伝播
をご覧ください。
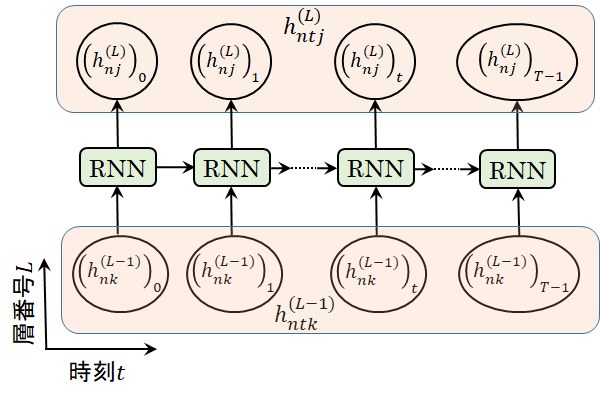
図5 RNN層の時刻要素登録の図式表現
RNNによる文章生成例
RNNの詳細は上記に説明した通りですが、自然言語処理の中でRNN層がどのように使用されるのかを見て行きましょう。
文章のサンプルとして、
各時刻における各層の状態は、
One-hotベクトルによる文章表現
のページでOne-hotベクトルで表現した「今日(2)/は(3)/晴れ(4)/です(5)/ね(6)/。(7)」を使用しましょう。
( )中の番号は単語IDであり、あらかじめ特殊語として全角スペース' 'を単語ID=0、'<eos>'を単語ID=1としてそれぞれ登録していることは前記ページで既に記述しました。
RNN層を用いてこの文章をを生成する場合には、図6のようなイメージになります。
RNNを用いた言語モデルにより文章を生成する場合には最初の単語を与えると、RNNが学習した文章により重みやバイアスが最適化されていますので、
次に出現する可能性が高い単語を出力します。そして、次の時刻ステップにはこの出力された単語を入力として与えることにより、順次文章を生成して生成して行きます。
しかし、
自然言語処理用AIの歴史
で述べた通り、このような言語モデルでは、実用に耐えうる汎用性はないと言えるでしょう。
ここに記載したRNNによる文章生成例では、最初に'<eos>'という記号を与えているだけで、文章生成のヒントになるような単語は与えていませんので、
このままでは適正な文章が生成されないことは容易に理解できるでしょう。
図6に示したRNN層を用いた文章生成は単なるイメージあり、
本サイトの最終ターゲットであるAttentionというEncoder-Decoderモデルに到達するには、もう少し工夫が必要なのです。
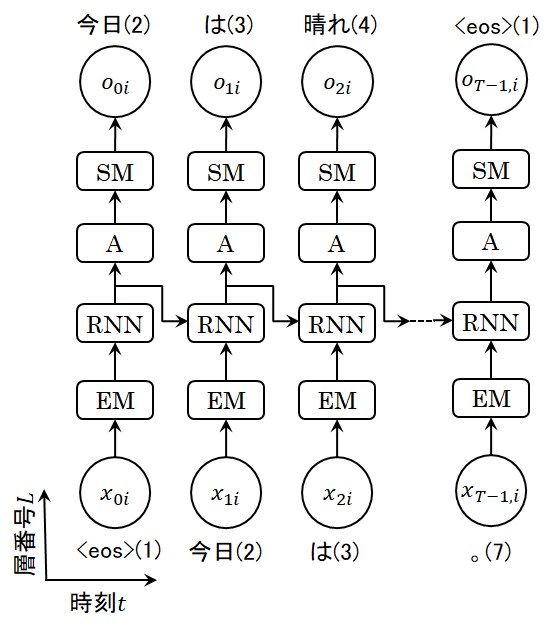
図6 RNN層を用いた文章生成
RNNの課題とその解決方法 - ゲート付きRNN
上述したRNNには、長期依存性のある言語モデルの学習(Learning long term dependencies)において、勾配消失(vanishing gradients)と勾配爆発(exploding gradients)という大きな課題を抱えています。
勾配消失や勾配爆発は、
誤差逆伝播法
を使用して図6に示すようなシステムで学習を行う際に、文章が長くなると誤差(勾配)が途中でゼロになったり、誤差の絶対値が大きくなり過ぎて発散してしまったりする現象です。
図7に示す通りtanh関数は変数\(x\)の絶対値が大きくなるとゼロに近づいてしまいますので、勾配消失が起こりそうであることは直感的に容易に理解できるでしょう。
また、文章が長くなると、誤差が(1)式の行列の積(\(h_{t-1,i}^{(L)} w_{ij}^{(L)}\))の項を何度も逆伝搬することになり、その度に同じ重み\(w_{ij}^{(L)}\)が掛けられますので、
誤差が一気に増幅してしまうこともは直感的に理解できるでしょう。
RNNが長期依存性のある時系列データの学習において勾配消失や勾配爆発を起こすことは経験的に古くから知られていましたが、
これを理論的に証明したのは
Y.Bengioら(1994)です。
ニューラルネットワークの学習には勾配降下法(Gradient Descendant)が使用されますが、文脈の長期依存性が必要である場合、
tanh関数を使用したRNNが入力ノイズに対して弱い(ロバストでない)か、あるいは勾配降下法による効率的な学習ができないということを彼らは理論的かつ実験的に示しました。
そして、このような研究が勾配クリッピングやLSTMへの開発へと発展して行きます。
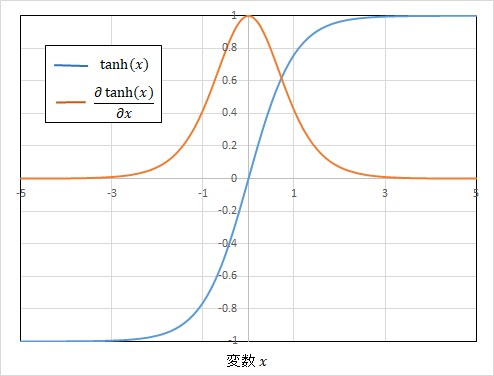
図7 tanh関数とその勾配
勾配爆発の解決方法
勾配爆発を解決する方法としては、
勾配クリッピング(Gradient Clipping)
が多くのの論文で活用されています。
勾配クリッピングとは、誤差(勾配)が途中である閾値(threshold:しきいち)\(\Theta\)を超えた場合には、この値を超えないよう\(\Theta\)に制限するというものです。
一般的に誤差はベクトルやテンソルですので、
RNN層の誤差逆伝播
に示す誤差\(\Delta w_{ij}^{(L)}\)の勾配クリッピングは、誤差のL2ノルム(平均二乗誤差)\( \| \Delta w_{ij}^{(L)} \| \)を使用して次式で表されます。
\[
w_{ij}^{(L)} \gets \frac{\Theta}{\| \Delta w_{ij}^{(L)} \|} w_{ij}^{(L)} \quad (\mathrm{If} \ \| \Delta w_{ij}^{(L)} \| > \Theta) \tag{7}
\]
LSTMによる勾配消失の解決方法
LSTMの基本的な考え方
LSTM(Long Short-Term Memory:長期の短期記憶を備えたニューラルネットワーク)という手法は、
LONG SHORT-TERM MEMORY(1997)という論文でHochreiterとSchmidhuberにより発表された後、
様々な人の改良により洗練されて現在では広く活用されている手法です。
LSTMではRNNの弱点である長期依存性のある言語モデルの学習おける勾配消失が起こりにくくなっていますので、ここでこの技術をご紹介しましょう。
なお、LSTMに関しては、
Understanding LSTM Networks(2015)
に詳しく説明されていますので一度ご覧になると良いでしょう。
バッチ処理を考慮したLSTMを図式表現すると図8のようになります。ここで、バッチ処理の復習をしたい方は
RNNの実装 - バッチ処理をご覧ください。
RNNでは時刻\(t\)方向の情報の流れは隠れ層の状態を表す\(h_{ntj}^{(L)}\)の一本だけでしたが、
LSTMではセル状態(cell state)を記憶する情報の流れ\(C_{ntj}^{(L)}\)が加わっています。
そして、セル状態を記憶する情報の流れは、隠れ層の状態の流れに比較すると、とても単純であることがわかります。
そして、この単純さが長い文章の学習おける勾配消失を起こりにくくしている最大の要因になっています。
図式表現中の演算\(\odot\)は同一形状の行列の要素ごとを掛け合わせるアダマール積を意味しますが、3か所で使用されているこの演算が情報の流れる量をコントロールしていますので、
LSTMがゲート付きRNNと呼ばれている理由です。
これらの3か所のゲートでは、入力をアフィン変換した変数行列\(A_{ntj}^{(L)}\)を部分行列に分割し、
ニューラルネットワークの数式表現
の項で説明したシグモイド関数\(\sigma\)で0~1に正規化してゲートの流れをコントロールしています。
即ち、シグモイド関数の出力が0に近い場合はその経路の情報を流れにくくし、1に近い場合はその経路の情報を流れやすくしてコントロールしているのです。
そして、3か所のゲートは、時刻\(t-1\)のセル状態\(C_{n,t-1,j}^{(L)}\)の情報の流れをコントロールする「忘却ゲート(goraget gater)」\(f_{ntj}^{(L)}\)、
活性化関数(tanh関数)で正規化した時刻\(t\)におけるセル状態の新たな候補\(\tilde{C}_{ntj}^{(L)}\)の流れをコントロールする
「入力ゲート(input gate)」\(i_{ntj}^{(L)}\)、
tanh関数で正規化した時刻\(t\)におけるセル状態\(C_{ntj}^{(L)}\)の情報を隠れ層の状態\(h_{ntj}^{(L)}\)へと伝達する流れをコントロールする
「出力ゲート(output gate)」\(o_{ntj}^{(L)}\)という3種類のゲートで構成されています。
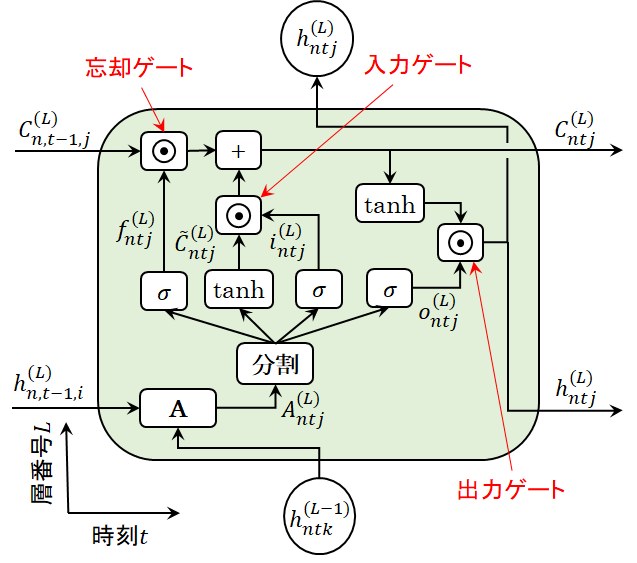
図8 LSTM層の図式表現
上記で解説したLSTMはごく一般的なLSTMですが、LSTMには
ゲートのコントロールに\(C_{n,t-1,j}^{(L)}\)や\(C_{ntj}^{(L)}\)の情報も使うような「覗き穴(peephole)」を設けたLSTM、
「忘却ゲート」と「入力ゲート」を共有するタイプのLSTMなど様々な改良版があります。
その中でも、「覗き穴」の導入や「忘却ゲート」と「入力ゲート」の共有などをさらに進めてセル状態を記憶する情報の流れ\(C_{ntj}^{(L)}\)を完全に除去した
Choらの研究(2014)は、GRU(Gated Recurrent Unit)として広く知られています。
LSTM層の実装
図8に示す一般的なLSTMはRNNに比較するとかなり複雑になっていますので、実装が大変だと思う方は多いでしょう。
しかし、アフィン変換\(A_{ntj}^{(L)}\)後の演算が多少複雑になっているだけであり、とても簡単なのです。
実装はRNN層と同様、最初にLSTM層の単一時刻における処理の実装を行い、その後LSTM層の時系列行列の設定を行います。
LSTM層の時系列行列の設定は、RNN層の時系列行列の設定と全く同じですので、ここではLSTM層の単一時刻における処理の実装についてのみ解説します。
まず、アフィン変換後の時刻\(t\)要素は次式で表現できます。
\begin{align}
(A_{nj}^{(L)})_t^{(l)} &= (h_{ni}^{(L)})_{t-1} (w_{ij}^{(L)})^{(l)} + (h_{nk}^{(L-1)})_t (w_{kj}^{(L-1)})^{(l)} + (b_{nj}^{(L)})^{(l)} \nonumber \\
&= \begin{pmatrix} (A_{nj}^{(L)})_t^{(F)} & (A_{nj}^{(L)})_t^{(C)} & (A_{nj}^{(L)})_t^{(I)} & (A_{nj}^{(L)})_t^{(O)} \end{pmatrix} \tag{8}
\end{align}
\begin{align}
&\begin{pmatrix} (f_{nj}^{(L)})_t & (\tilde{C}_{nj}^{(L)})_t & (i_{nj}^{(L)})_t & (o_{nj}^{(L)})_t \end{pmatrix} \nonumber \\
&= \begin{pmatrix} \sigma((A_{nj}^{(L)})_t^{(F)}) & \tanh((A_{nj}^{(L)})_t^{(C)}) & \sigma((A_{nj}^{(L)})_t^{(I)}) & \sigma((A_{nj}^{(L)})_t^{(O)}) \end{pmatrix} \tag{9}
\end{align}
ここで、\((l)\)は、忘却ゲート(\(F\))、セル状態の新たな候補(\(\tilde{C}\)の代用として\(C\))、入力ゲート(\(I\))、出力ゲート(\(O\))の4種類の変数であることを意味しています。
また、各重みやバイアスは次式で与えられます。
\[
(w_{ij}^{(L)})^{(l)} = \begin{pmatrix} (w_{ij}^{(L)})^{(F)} & (w_{ij}^{(L)})^{(C)} & (w_{ij}^{(L)})^{(I)} & (w_{ij}^{(L)})^{(O)} \end{pmatrix} \tag{10}
\]
\[
(w_{kj}^{(L-1)})^{(l)} = \begin{pmatrix} (w_{kj}^{(L-1)})^{(F)} & (w_{kj}^{(L-1)})^{(C)} & (w_{kj}^{(L-1)})^{(I)} & (w_{kj}^{(L-1)})^{(O)} \end{pmatrix} \tag{11}
\]
\[
(b_{nj}^{(L)})^{(l)} = \begin{pmatrix} (b_{nj}^{(L)})^{(F)} & (b_{nj}^{(L)})^{(C)} & (b_{nj}^{(L)})^{(I)} & (b_{nj}^{(L)})^{(O)} \end{pmatrix} \tag{12}
\]
最終的な出力は、ゲートのアダマール積\(\odot\)を使用して次式で求められます。
\[
(C_{nj}^{(L)})_t = (f_{nj}^{(L)})_t \odot (C_{nj}^{(L)})_{t-1} + (\tilde{C}_{nj}^{(L)})_t \odot (i_{nj}^{(L)})_t \tag{13}
\]
\[
(h_{nj}^{(L)})_t = (o_{nj}^{(L)})_t \odot \tanh((C_{nj}^{(L)})_t) \tag{14}
\]
そして、(8)式~(14)式は、機械語レベルで配列の高速処理が可能なNumPyやGPUで配列の並列処理が可能なCuPyを使用すれば、
以下に示すようなをforward()というとてもシンプルなPythonの関数として実装することができます。
#GPUの場合にはCuPyをnpという変数で使用、それ以外はNumPyをという変数で使用する
if GPU:
import cupy as np
else:
import numpy as np
・・・
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def forward(self, h_Lm1, h_tm1, C_tm1):
#内部パラメータを重み変数とバイアス変数にセット
W_Lm1, W_L, b_L = self.params
#L層のh配列サイズの取得→A配列から部分配列の取り出しに使用
N, H = h_tm1.shape
#(8)式→配列サイズh_tm1:HxH, W_L:Hx4H, h_Lm1:DxH, W_Lm1:Hx4H
#numpy配列の積はnp.dot(h, W)で表現できます。
A = np.dot(h_tm1, W_L) + np.dot(h_Lm1, W_Lm1) + b_L
#(9)式→A配列から部分配列に分割
F = sigmoid(A[:, :H])
C = np.tanh(A[:, H:2*H])
I = sigmoid(A[:, 2*H:3*H])
O = sigmoid(A[:, 3*H:])
#(13)式,(14)式:numpy配列のアダマール積は'*'で表現できます。
C_t = F * C_tm1 + C * I
h_t = O * np.tanh(C_t)
#内部変数の更新
self.caches = (h_Lm1, h_tm1, C_tm1, F, C, I, O, C_t)
#戻り値の設定
return h_t, C_t
なお、LSTM層を実装するためにはLSTM層の誤差逆伝播も数式表現する必要があります。
LSTM層の誤差逆伝播の詳細は、
LSTM層の誤差逆伝播
をご覧ください。
LSTM以外の勾配消失の解決方法
前述の通り勾配消失はtanh関数に起因していますので、tanh関数を別の関数に変更するというアイデアも実施されています。
その他の活性化関数
の項で活性化関数として単純なReLU関数(Rectified Linear Unit)を使用したモデルの方がtanh(x)を使用したモデルよりも誤差の低下速度が速いことを示したXavier Glorotらの研究をご紹介しましたが、
tanh(x)の代わりにReLU関数を使用するのも良いアイデアでしょう。










-172.31.37.45。