誤差逆伝播法（Back-propagation of Errors）は、 David E. Rumelhartらの論文Learning representations by back-propagating errors(1986)以降、 ニューラルネットワークのディープラーニング（深層学習）手段として定着して行きました。 誤差逆伝播とは、各層の状態変数の誤差が、あたかも上流側に逆伝播するような振舞いであり、 ニューラルネットワークを実装する際にはこの振舞を利用した誤差逆伝播法が不可欠ですので、忘備録の意味も兼ねてこのページにまとめておきましょう。

1. 誤差逆伝播法概要
2. 誤差逆伝播法の基本的な考え方
3. 様々な演算の誤差逆伝播
   • 加算演算の誤差逆伝播
   • 乗算演算の誤差逆伝播
   • 分岐演算の誤差逆伝播
   • Affine層の誤差逆伝播
   • Embedding層の誤差逆伝播
   • RNN層の誤差逆伝播
     • RNN層の単一時刻における誤差逆伝播
     • RNN層の時系列行列の誤差逆伝播
   • LSTM層の誤差逆伝播

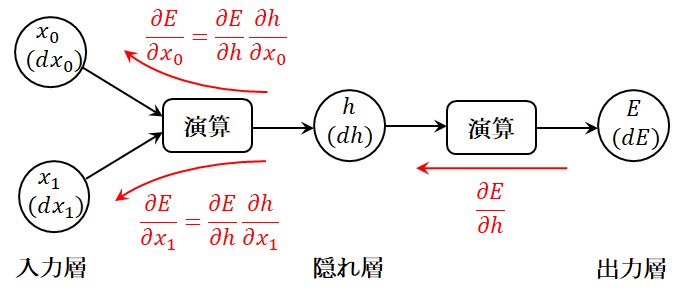
   図1に示すような二層ニューラルネットワークについて考えてみましょう。 一般的には出力状態\(E\)を除き、入力状態や中間層の状態はベクトルとなりますが、ここでは理解しやすくするために全てスカラー値として 入力状態\(x_0\),\(x_1\)、中間層の状態\(h\)、出力状態\(E\)としています。 そして、損失関数である クロスエントロピー誤差 を最小にするような重みやバイアスを求めることがニューラルネットワークの学習に相当します。 入力状態、中間層の状態、出力状態の微小な変動\(dx_0, dx_1, dh\)が\(dE\)へどように伝わって行くかは(1)式および(2)式で表されます。

\begin{align} dh &= \frac{\partial h}{\partial x_0} dx_0 + \frac{\partial h}{\partial x_1} dx_1 \tag{1} \\ dE &= \frac{\partial E}{\partial h} dh = \frac{\partial E}{\partial h}(\frac{\partial h}{\partial x_0} dx_0 + \frac{\partial h}{\partial x_1} dx_1) \nonumber \\ &= \frac{\partial E}{\partial x_0} dx_0 + \frac{\partial E}{\partial x_1} dx_1 \tag{2} \end{align}

(1)式、(2)式および図1から、隠れ層の変化に対する出力層の変化の割合（勾配）\({\partial E}/{\partial h}\)に、 入力層の変化に対する隠れ層の変化の割合\({\partial h}/{\partial x_0}\)および\({\partial h}/{\partial x_1}\)を掛け合わせたものが、 入力層の変化に対する出力層の変化の割合になっていることがわかります。 即ち、各層の状態の変化を表す勾配（偏微分）が、掛け合わせることにより上流に逆伝播しているように振舞っていますので、 この基本原理を用いてクロスエントロピー誤差から重みやバイアスを逐次修正して行く方法が誤差逆伝播法（back-propagation of errors）と呼ばれています。

   ここでは、ニューラルネットワークで一般的に使用される演算について、誤差逆伝播についてまとめておきます。

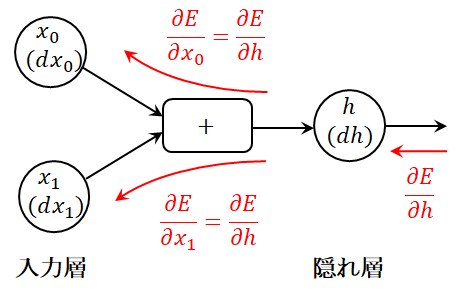
   図2に示す加算演算では、 \[ h = x_0 + x_1 \tag{3} \] \[ \frac{\partial h}{\partial x_0} = \frac{\partial h}{\partial x_1} = 1 \tag{4} \] という関係から、誤差逆伝播は下流の勾配が上流側に通過して行くだけです。 これは加算演算する状態変数の数が増加しても同じことになります。

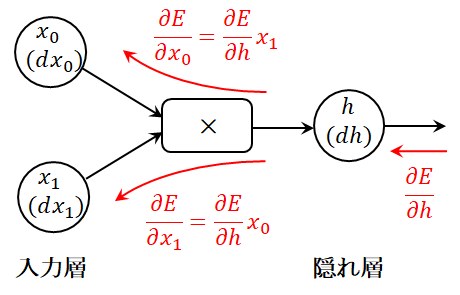
   図3に示す乗算演算では、 \[ h = x_0 x_1 \tag{5} \] \[ \frac{\partial h}{\partial x_0} = x_1, \frac{\partial h}{\partial x_1} = x_0 \tag{6} \] という関係から、誤差逆伝播は下流の勾配に乗算する相手の変数を乗算するだけです。

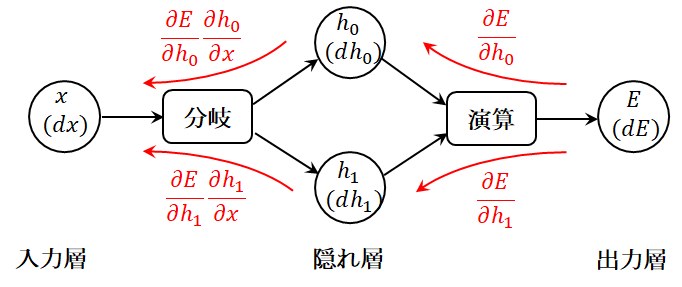
   図4に示す分岐演算では、入力層の状態\(x\)が中間層へそのままコピーされて中間層の値になりますので、 \[ h_0 = h_1 = x \tag{7} \] となります。そして、出力層の状態\(E\)は入力層の状態変数\(x\)を使用して \[ E = E(h_0(x), h_1(x)) \tag{8} \] のように表示されますので、これを\(x\)で微分すれば、 \[ \frac{\partial E}{\partial x} = \frac{\partial E}{\partial h_0} \frac{\partial h_0}{\partial x} + \frac{\partial E}{\partial h_1} \frac{\partial h_1}{\partial x} \tag{9} \] となります。即ち、分岐演算では勾配が加算されることになります。 これは分岐演算する状態変数の数が増加しても同じことになります。

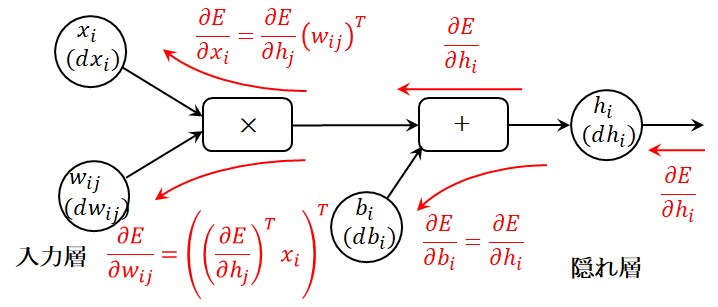
   ここでは、Affine変換を行う Affine層 についての誤差逆伝播をまとめておきましょう。 上記とは異なり、各層の状態変数、重み、バイアスなどのパラメータはスカラー値ではなく、 図5に示す通りベクトルや行列になりますが、誤差逆伝播の基本的な考え方はスカラー値の場合と同じです。 ただし、注意すべきことは、\(x_i\)、\(h_j\)、\(b_j\)は行ベクトルであり、\({\partial E}/{\partial h_j}\)も\(h_j\)と同次元の行ベクトルになるという点です。 そして、ベクトルや行列の形状に注意しながら、上記の加算演算や乗算演算の知識を使えば、次式を得ることができます。 ここで、右肩に\(T\)を付けて転置行列を表示していますので、\((w_{ij})^T\)は\(w_{ij}\)の転置行列を意味します。 \[ \frac{\partial E}{\partial b_j} = \frac{\partial E}{\partial h_j} \tag{10} \] \[ \frac{\partial E}{\partial w_{ij}} = ( (\frac{\partial E}{\partial h_j})^T x_i)^T = (x_i)^T \frac{\partial E}{\partial h_j} \tag{11} \] \[ \frac{\partial E}{\partial x_i} = \frac{\partial E}{\partial h_j} (w_{ij})^T = \frac{\partial E}{\partial h_j} w_{ji} \tag{12} \]

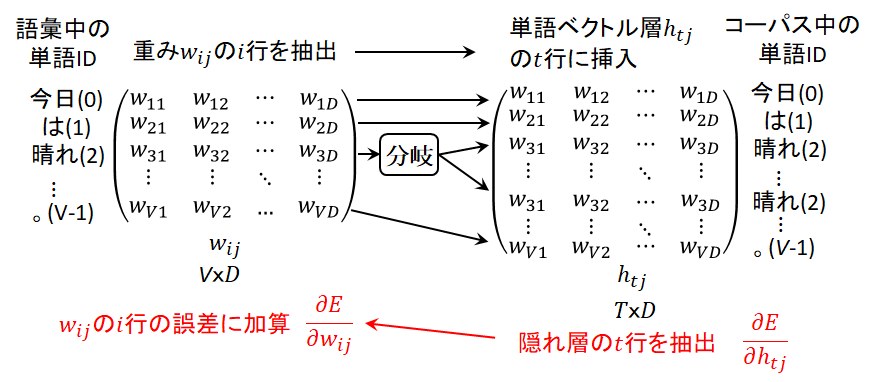
   ここでは、 One-hotベクトル によりコーパスを表現した場合の Embedding層 の誤差逆伝播をまとめておきましょう。 Embedding層の演算は、重み\(w_{ij}\)の\(i\)行を抽出して隠れ層（単語ベクトル層）の\(t\)行に挿入するというものです。 ここで、\(i\)行とはコーパスをOne-hot表現した際の単語ID列を意味していて、\(i = 0\) ～ \(V - 1\)の値を取りますが、 \(V\)はそのシステムにおける語彙数ですので、採用しているシステムにより数万～100万語程度とかなり大きな値となります。

そして、単語ベクトル層の\(t\)行に挿入の際、コーパス中に同一単語が複数回出てきた場合には図6に示す通り分岐演算することになりますので、 分岐演算の誤差逆伝播の項で説明した通り、その逆伝播は誤差を加算することになります。 即ち、隠れ層の\(t\)行の誤差を抽出して重み\(w_{ij}\)の\(i\)行の誤差に加算して行くということがEmbedding層の誤差逆伝播になります。

   RNNの実装 - バッチ処理 で述べた通り、RNNの実装の際には大量のデータをまとめて処理するバッチ処理が行われますが、その際にはバッチ処理の部分と時刻処理の部分を切り離して処理することになります。 RNN層の誤差逆伝播もこの考えに従って計算して行きます。

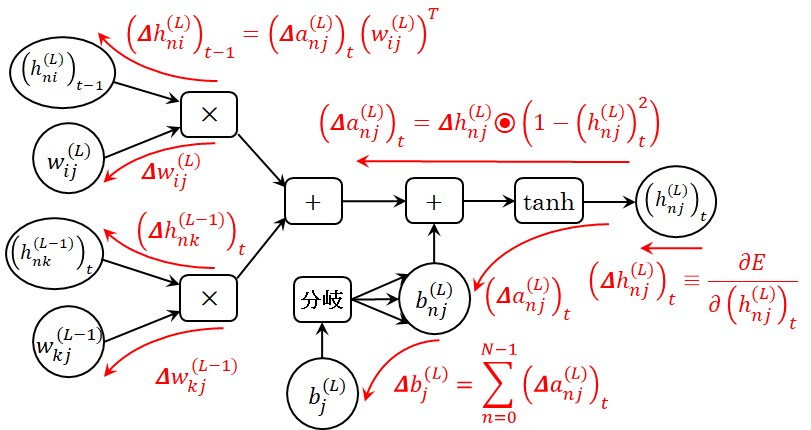
   まず、バッチ処理を行う際の単一時刻における誤差逆伝播についてまとめておきましょう。 RNN層の単一時刻における処理 の(5)式に従えば、RNN層の計算情報の流れや誤差の逆伝播は図7のように表現できます。ここでは表現を簡単化するため、第\(L\)層である隠れ層に下流側から伝播する誤差を次式で定義します。 \[ (\Delta h_{nj}^{(L)})_t \equiv \frac{\partial E}{\partial (h_{nj}^{(L)})_t} \tag{13} \] ここで、時刻\(t\)の要素を\(( )_t\)と表現していますので、\((h_{nj}^{(L)})_t\)は\(h_{ntj}^{(L)}\)の時刻\(t\)の要素であることを意味しています。そして、 \[ \frac{\partial \tanh(x)}{\partial x} = 1 - (\tanh(x))^2 \tag{14} \] の関係を使用すると\(\tanh\)の演算をする前の誤差\((\Delta a_{nj}^{(L)})_t\)は、 \[ (\Delta a_{nj}^{(L)})_t = (\Delta h_{nj}^{(L)})_t \odot ( 1 - (h_{nj}^{(L)})_t^2 ) \tag{15} \] となります。ここで、\(\odot\)は同一形状の行列の要素ごとを掛け合わせるアダマール積を意味しますが、 \(\tanh\)関数が行列の要素ごとに作用しているため、逆伝播も要素ごとを掛け合わせるアダマール積が使用されることになります。 RNN層の単一時刻における処理 の(5)式の解説で述べた通り、第\(L\)層のバイアス\(b_{j}^{(L)}\)はバッチ変数\(n\)には無関係なパラメータですが、 隠れ層の状態\((h_{nj}^{(L)})_t\)と次元を一致させるためNumPyのブロードキャストという機能を使用して\(n\)方向に値をコピーしています。 このため、\(b_{j}^{(L)}\)へ伝播する誤差は分岐演算の誤差逆伝播と同様、\(n\)方向に値を加算して求められます。 \[ \Delta b_{j}^{(L)} = \displaystyle \sum_{ n = 0 }^{ N - 1 } (\Delta a_{nj}^{(L)})_t \tag{16} \]

さらに、第\(L-1\)層および時系列変数\(t-1\)の隠れ層の状態変数や重みへ逆伝播する誤差は、次式で表すことができます。 ここで、右肩に\(T\)を付けて転置行列を表示していますので、\((w_{ij}^{(L)})^T\)は\(w_{ij}^{(L)}\)の転置行列を意味します。 \[ \Delta w_{ij}^{(L)} = ( ((\Delta a_{nj}^{(L)})_t)^T (h_{ni}^{(L)})_{t-1} )^T = ((h_{ni}^{(L)})_{t-1})^T (\Delta a_{nj}^{(L)})_t \tag{17} \] \[ \Delta (h_{ni}^{(L)})_{t-1} = (\Delta a_{nj}^{(L)})_t (w_{ij}^{(L)})^T \tag{18} \] \[ \Delta w_{kj}^{(L-1)} = (((\Delta a_{nj}^{(L)})_t)^T (h_{nk}^{(L-1)})_{t})^T = ((h_{nk}^{(L-1)})_{t})^T \Delta (a_{nj}^{(L)})_t \tag{19} \] \[ \Delta (h_{nk}^{(L-1)})_t = (\Delta a_{nj}^{(L)})_t (w_{kj}^{(L-1)})^T \tag{20} \]

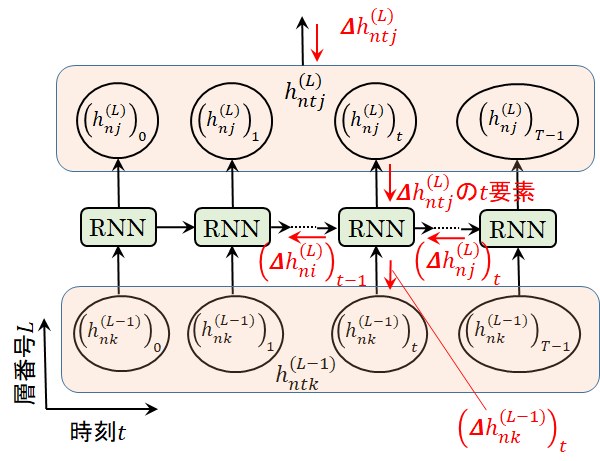
   以上で、時刻\(t\)におけるRNN層の各要素の逆伝播が計算ができました。 時刻\(t\)におけるRNN層の誤差逆伝播では、内部変数である重み\(\Delta w_{ij}^{(L)}\), \(\Delta w_{kj}^{(L-1)}\)、バイアス\(\Delta b_{j}^{(L)}\)、 そして、外部出力である誤差変数\((\Delta h_{ni}^{(L)})_{t-1}\), \((\Delta h_{nk}^{(L-1)})_t\)が計算できましたので、後は図8に示す通りこれらの要素を時系列行列として設定するだけですが、 見落としがちな二点の注意点を示しておきましょう。

第一の注意点は、RNN層の時刻\(t\)における誤差逆伝播の入力は、RNN層の次層から逆伝播した\(\Delta h_{ntj}^{(L)}\)の時刻\(t\)要素とRNN層内の時刻\(t+1\)から逆伝播した\((\Delta h_{nj}^{(L)})_t\) を加算した値を使用して、次式のように与えなければなりません。 ここで、\(BW ( )\)は、RNN層の単一時刻における誤差逆伝播の式である(16)式から(20)式をまとめて表示した関数と考えてください。 RNN層の単一時刻における処理 の図4に示す通り、RNN層の時刻t要素の出力は2つに分岐していますので、その逆伝播は加算することになります。 \[ \Delta w_{ij}^{(L)}, \Delta w_{kj}^{(L-1)}, \Delta b_{j}^{(L)}, (\Delta h_{ni}^{(L)})_{t-1}, (\Delta h_{nk}^{(L-1)})_t \gets BW ( \Delta h_{ntj}^{(L)}の時刻t要素 + (\Delta h_{nj}^{(L)})_t ) \tag{21} \]

もう一つの注意点は、逆伝播した重み\(\Delta w_{ij}^{(L)}\), \(\Delta w_{kj}^{(L-1)}\)やバイアス\(\Delta b_{j}^{(L)}\)は、時刻\(t\)に関して合計を取る必要がある点です。 これは、RNNの数式表現 の(1)式で解説した通り、\(t\)方向には毎回同じ重み\(w_{ij}^{(L)}\), \(w_{kj}^{(L-1)} \)やバイアス\(b_{j}^{(L)}\)が使用されること、 即ち、\(t\)方向に重みやバイアスが分岐していることに相当しているためです。

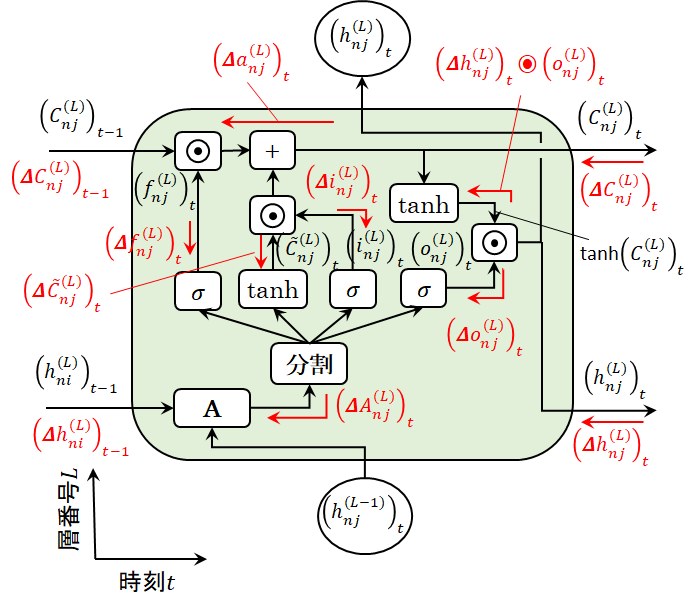
   LSTMによる勾配消失の解決方法 で述べた通り、LSTMはRNNの弱点であった長期依存性のある言語モデルの学習おける勾配消失が起こりにくくなっていますので、広く活用されている技術です。 ここでは、このLSTM層の誤差逆伝播についてまとめておきましょう。 LSTM層の時系列行列の誤差逆伝播はRNN層と同じですので、ここではLSTM層の単一時刻における誤差逆伝播のみ記述しておきます。

(14)式の関係を使用すると忘却ゲートの下流側の誤差\((\Delta a_{nj}^{(L)})_t\)は、次式で表されます。 \[ (\Delta a_{nj}^{(L)})_t = (\Delta C_{nj}^{(L)})_t + (\Delta h_{nj}^{(L)})_t \odot (o_{nj}^{(L)})_t \odot ( 1 - (\tanh(C_{nj}^{(L)})_t)^2 ) \tag{22} \] この値を用いると、時刻\(t-1\)のセル状態へ逆伝播する誤差\((\Delta C_{nj}^{(L)})_{t-1}\)、 tanh関数やシグモイド関数を通過後のセル状態の新たな候補やゲートへ逆伝播する誤差などは次式で表現されます。 \[ (\Delta C_{nj}^{(L)})_{t-1} = (\Delta a_{nj}^{(L)})_t \odot (f_{nj}^{(L)})_t \tag{23} \] \[ (\Delta f_{nj}^{(L)})_t = (\Delta a_{nj}^{(L)})_t \odot (C_{nj}^{(L)})_{t-1} \tag{24} \] \[ (\Delta \tilde{C}_{nj}^{(L)})_t = (\Delta a_{nj}^{(L)})_t \odot (i_{nj}^{(L)})_{t} \tag{25} \] \[ (\Delta i_{nj}^{(L)})_t = (\Delta a_{nj}^{(L)})_t \odot (\tilde{C}_{nj}^{(L)})_t \tag{26} \] \[ (\Delta o_{nj}^{(L)})_t = (\Delta h_{nj}^{(L)})_t \odot \tanh(C_{nj}^{(L)})_t \tag{27} \]

(14)式およびシグモイド関数の微分関係式 \[ \frac{\partial \sigma(x)}{\partial x} = \sigma(x) ( 1 - \sigma(x)) \tag{28} \] を使用すれば、アフィン層へ伝わる誤差は、次式のようにまとめることができます。 \[ (\Delta A_{nj}^{(L)})_t^{(F)} = (\Delta f_{nj}^{(L)})_t \odot (f_{nj}^{(L)})_t \odot (1 - (f_{nj}^{(L)})_t) \tag{29} \] \[ (\Delta A_{nj}^{(L)})_t^{(C)} = (\Delta \tilde{C}_{nj}^{(L)})_t \odot (1 - (\tilde{C}_{nj}^{(L)})_t^2) \tag{30} \] \[ (\Delta A_{nj}^{(L)})_t^{(I)} = (\Delta i_{nj}^{(L)})_t \odot (i_{nj}^{(L)})_t \odot (1 - (i_{nj}^{(L)})_t) \tag{31} \] \[ (\Delta A_{nj}^{(L)})_t^{(O)} = (\Delta o_{nj}^{(L)})_t \odot (o_{nj}^{(L)})_t \odot (1 - (o_{nj}^{(L)})_t) \tag{32} \] \[ (\Delta A_{nj}^{(L)})_t = \begin{pmatrix} (\Delta A_{nj}^{(L)})_t^{(F)} & (\Delta A_{nj}^{(L)})_t^{(C)} & (\Delta A_{nj}^{(L)})_t^{(I)} & (\Delta A_{nj}^{(L)})_t^{(O)} \end{pmatrix} \tag{33} \]

以上でアフィン変換後の誤差行列\((\Delta A_{nj}^{(L)})_t\)が計算できましたので、その前にあるアフィン変換の逆伝播はRNN層の(16)式～(20)式をLSTMの変数を使用して書き直すだけです。 そして、第\(L-1\)層や時系列変数\(t-1\)の隠れ層の状態変数、重みやバイアスへ逆伝播する誤差は以下のように表すことができます。 ここで、右肩に\(T\)を付けて転置行列を表示していますので、\((w_{ij}^{(L)})^T\)は\(w_{ij}^{(L)}\)の転置行列を意味します。 \[ \Delta b_{j}^{(L)} = \displaystyle \sum_{ n = 0 }^{ N - 1 } (\Delta A_{nj}^{(L)})_t \tag{34} \] \[ \Delta w_{ij}^{(L)} = ( ((\Delta A_{nj}^{(L)})_t)^T (h_{ni}^{(L)})_{t-1} )^T = ((h_{ni}^{(L)})_{t-1})^T (\Delta A_{nj}^{(L)})_t \tag{35} \] \[ \Delta (h_{ni}^{(L)})_{t-1} = (\Delta A_{nj}^{(L)})_t (w_{ij}^{(L)})^T \tag{36} \] \[ \Delta w_{kj}^{(L-1)} = (((\Delta A_{nj}^{(L)})_t)^T (h_{nk}^{(L-1)})_{t})^T = ((h_{nk}^{(L-1)})_{t})^T \Delta (A_{nj}^{(L)})_t \tag{37} \] \[ \Delta (h_{nk}^{(L-1)})_t = (\Delta A_{nj}^{(L)})_t (w_{kj}^{(L-1)})^T \tag{38} \]

そして、(22)式～(38)式は、機械語レベルで配列の高速処理が可能なNumPyやGPUで配列の並列処理が可能なCuPyを使用すれば、 以下に示すようなをbackward()というとてもシンプルなPythonの関数として実装することができます。