AIとは - ニューラルネットワーク

AIゆめ
AI(Artificial Intelligence:人工知能)とは、知的な問題解決能力を持った脳のニューロン(neuron:神経細胞)を模擬したシステムのことであり、
下記で説明するニューラルネットワークと同義と考えて良いでしょう。
ニューロンは図1に示す通り核がある細胞体(cell body)、
細胞体から伸びる軸索(axon)、軸索の先端にあるシナプス(synapse)を介して隣にあるニューロンと繋がっている樹状突起(dendrite)から構成されていて、
成人のニューロンの数は100億~1000億程度と言われています。
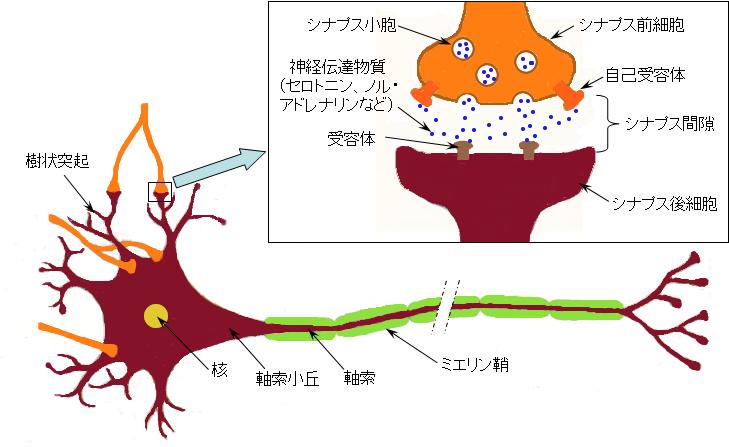
図1 ニューロンによる情報伝達
そして、細胞体で何らかの計算を行い、その計算情報は電気信号として軸索(axon)を通じて伝送され、シナプスで化学物資を放出することにより隣にある細胞体の樹状突起へと伝達されて行きます。
ニューラルネットワークは、この計算情報の流れを模擬したシステムであり、図2に示す通り入力層、隠れ層(中間層と呼ばれることもあります)、出力層で構成されています。
これらの層がニューロンの細胞体に該当し、情報の流れを表す矢印が軸索に該当すると考えると良いでしょう。
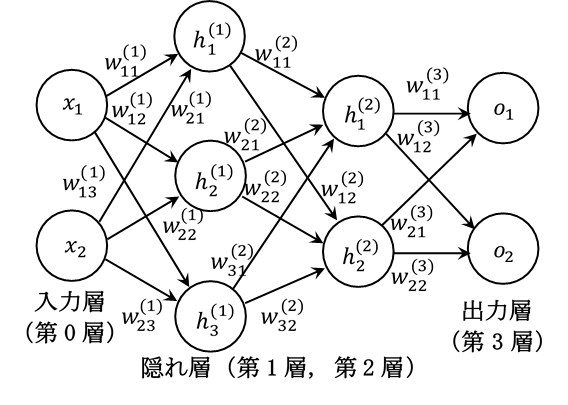
図2 三層ニューラルネットワーク
ニューラルネットワークの最大の特徴は自分で学習するという点です。
図2の\(x_{1}\)、\(x_{2}\)はニューラルネットワークへの入力層の状態、\(h_{1}^{(1)}\)~\(h_{3}^{(1)}\)および\(h_{1}^{(2)}\)~\(h_{3}^{(2)}\)は隠れ層の状態、
\(o_{1}\)、\(o_{2}\)は出力層の状態です。
そして、\(w_{11}^{(1)}\)~\(w_{23}^{(1)}\)、\(w_{11}^{(2)}\)~\(w_{32}^{(2)}\)、\(w_{11}^{(o)}\)~\(w_{22}^{(o)}\)は重みと呼ばれるパラメータですが、
この重みが決まれば入力層の状態に対応する出力層の状態が決まりますので、最適な重みを求めることが学習するという行為になります。
図2は情報の変換が三回行われますので、本サイトでは三層ニューラルネットワークと呼びます。
人間の脳と同様、ニューラルネットワークの層を深くすることにより、より複雑な課題に柔軟に対応できることが知られています。
そして、深いニューラルネットワークの最適な重みを求めることはディープラーニング(Deep Learning:深層学習)と呼ばれています。
ニューラルネットワークの目次
ニューラルネットワークの数式表現
一般的なニューラルネットワークを数式で表現してみましょう。
数式は苦手という方は多いと思いますが、ニューラルネットワークは微分、ベクトル、行列の数学知識さえあれば理解するのは難しくないと思います。
ベクトルや行列と言っても、このページで解説する比較的初歩的な知識で十分であり、表記ルールに慣れてしまえば意外に簡単なものですので、頑張って理解して行きましょう。
隠れ層の数式表現
まず、隠れ層を数式表現してみましょう。各層の状態を表すベクトルとして行ベクトルを使用しますが、例えば次式において\(x_i w_{ij}^{(1)}\)を\(w_{ji}^{(1)} x_i\)と書き換えれば、
各層の状態を列ベクトルとして捉えることも可能です。
\begin{align}
h_j^{(1)} &= x_i w_{ij}^{(1)} + b_j^{(1)} \tag{1}
\end{align}
\begin{align}
h_j^{(L)} &= \sigma(h_i^{(L-1)} w_{ij}^{(L)} + b_j^{(L)}) \nonumber \\ &= \frac{1}{1 + \exp( - ( h_i^{(L-1)} w_{ij}^{(L)} + b_j^{(L)} ) )}
\quad ( L > 1 ) \tag{2}
\end{align}
ここで、入力層の状態\(x_i\)は行ベクトル、\(w_{ij}^{(L)}\)は行列であり、
ニューラルネットワークの層番号を表す\((L)\)以外の同じ添え字が積の中に2回現れた時にはその添え字につい総和されるというアインシュタインの総和規約が適用されます。
幾何学の分野では、\(y_j = x_i w_{ij} + b_j\)という形式の変換はAffine変換と呼ばれ、
画像の並行移動、拡大や縮小、回転、せん断などの線型変換として使用されますので、(1)式のような変換を行う層はAffine層と呼ばれます。
アインシュタインの総和規約に馴染んでいない方のために、(1)式および(2)式に現れるAffine変換の部分を図2の例を用いて展開表記しておきましょう。
\begin{align}
x_i w_{ij}^{(1)} + b_j^{(1)} &= \displaystyle \sum_{ i = 1 }^{ 2 } x_i w_{ij}^{(1)} + b_j^{(1)} = \begin{pmatrix} x_1 & x_2 \end{pmatrix}
\begin{pmatrix} w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)} \\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)} \end{pmatrix} +
\begin{pmatrix} b_1^{(1)} & b_2^{(1)} & b_3^{(1)} \end{pmatrix} \nonumber \\
&= \begin{pmatrix} x_1 w_{11}^{(1)} + x_2 w_{21}^{(1)} + b_1^{(1)} & x_1 w_{12}^{(1)} + x_2 w_{22}^{(1)} + b_2^{(1)} & x_1 w_{13}^{(1)} + x_2 w_{23}^{(1)} + b_3^{(1)} \end{pmatrix}
\tag{3}
\end{align}
\begin{align}
h_i^{(1)} w_{ij}^{(2)} + b_j^{(2)} &= \displaystyle \sum_{ i = 1 }^{ 3 } h_i^{(1)} w_{ij}^{(2)} + b_j^{(2)} = \begin{pmatrix} h_1^{(1)} & h_2^{(1)} & h_3^{(1)} \end{pmatrix}
\begin{pmatrix} w_{11}^{(2)} & w_{12}^{(2)} \\ w_{21}^{(2)} & w_{22}^{(2)} \\ w_{31}^{(2)} & w_{32}^{(2)} \end{pmatrix} +
\begin{pmatrix} b_1^{(2)} & b_2^{(2)} \end{pmatrix} \nonumber \\
&= \begin{pmatrix} h_1^{(1)} w_{11}^{(2)} + h_2^{(1)} w_{21}^{(2)} + h_3^{(1)} w_{31}^{(2)} + b_1^{(2)} &
h_1^{(1)} w_{12}^{(2)} + h_2^{(1)} w_{22}^{(2)} + h_3^{(1)} w_{32}^{(2)} + b_2^{(2)} \end{pmatrix}
\tag{4}
\end{align}
また、\(\sigma(x)=1/(1+\exp(-x))\)はシグモイド関数と呼ばれ、隠れ層の状態\(h_j^{(L)}\)がどのように活性化するかを表しますので活性化関数(activation function)と呼ばれます。
脳のニューロンは、入力の状態がある条件の時に発火して隣のニューロンに情報を伝達しますが、
活性化関数もこの発火に類似していて、入力の状態がある条件を満足した時に、次のニューラルネットワークへ伝達する値が大きくなります。
シグモイド関数は図3に示すように、出力が0~1に正規化されています。
シグモイド関数は第一層で使用されることは殆どありませんが、第二層以降では使用されることがありますので、ここでは(2)式に導入して表記しています。
(1)式および(2)式では図2には表示されていないバイアスと呼ばれるパラメータ\(b_j^{(L)}\)が使用されていますが、バイアスは図3に示す通りシグモイド関数を横方向にシフト(かさ上げ)する働きがあります。
電気関係ではバイアスは電子部品に加える直流電流を意味する用語としてよく知られていますが、ここで導入されたバイアスにもこれと同様の機能があると考えて良いでしょう。
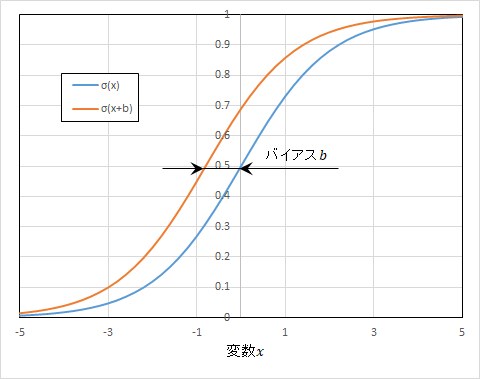
図3 シグモイド関数とバイアス
ニューラルネットワークの最大の特徴である自分で学習するという機能は、後述する誤差の逆伝播(backwards propagation of errors)により実現されます。
そして、この誤差逆伝播法を適用するためには、関数の勾配が解析的に求められるような非線形関数を用いることが重要な要素の一つになりますので、
この条件を満たすシグモイド関数などが使用されます。
その他の活性化関数
隠れ層の数式表現として(2)式ではシグモイド関数を使用しましたが、活性化関数はシグモイド関数だけではありませんので、ここでまとめておきましょう。
ニューラルネットワークの学習には
誤差逆伝播法
を使用しますので、活性化関数の必要条件としては、解析的に勾配が求められる非線形関数ということになります。
そして、シグモイド関数以外によく使用される活性化関数としては、
RNN(Recurrent Neural Network:再帰ニューラルネットワーク)
で使用されるハイパボリック・タンジェント(hyperbolic tangent)関数\(\tanh(x)\)でしょう。
\[
y = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)} \tag{5}
\]
ハイパボリック・タンジェント関数は、図4に示す通り出力を-1~1に正規化する活性化関数ですが、
シグモイド関数とは次式のような関係がありますので、これらの活性化関数はかなり類似した活性化関数と言えるでしょう。
\[
\sigma(x)=\frac{1}{1+\exp(-x)} = \frac{\tanh(\frac{x}{2}) + 1}{2} \tag{6}
\]
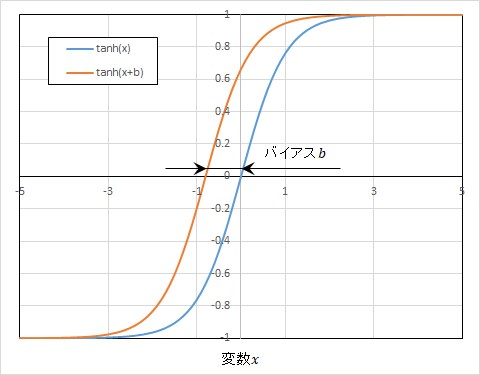
図4 ハイパボリック・タンジェント関数とバイアス
Xavier Glorotらは、
Deep Sparse Rectifier Neural Networks(2011年)
で、活性化関数として(7)式で表される単純なReLU関数(Rectified Linear Unit:ランプ関数のこと)を使用したモデルの方が\(\tanh(x)\)を使用したモデルよりも誤差の低下速度が速いことを示しました。
そして、この発表以降、ReLU関数を使用したモデルが増えて行きました。
特に、画像認識や音声認識などに活用されているCNN(Convolutional Neural Network:畳み込みニューラルネットワーク)では、
活性化関数としてReLU関数が標準の活性化関数になっていると言っても過言ではないでしょう。
\begin{eqnarray}
\max ( x, 0 ) = \begin{cases} x & ( x \gt 0 ) \\ 0 & ( x \leqq 0 ) \end{cases} \tag{7}
\end{eqnarray}
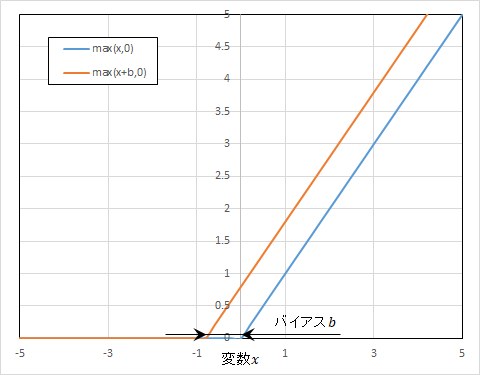
図5 ReLU関数とバイアス
出力層の数式表現
出力層は0~1に正規化されるケースとされないケースがあります。そして、正規化されないケースでは、出力層は次式のようなAffine変換で表示されます。
ここで、添え字\(t\)は言語モデルにおける時系列の単語の並びを想定したものです。
\[
o_t = h_i^{(L-1)} w_{it}^{(L)} + b_t^{(L)} \tag{8}
\]
単語の並びから次に来る単語を予測するような言語モデルでは、出力層の単語ベクトルの中から次に出現する可能性が最も高い単語を選ぶという課題に帰着されますので、
わざわざ正規化する必要がないケースと言えるでしょう。ただし、次に出現すると予測した単語がどの程度確からしいかを知る必要がある場合には、このケースでも正規化する必要があるでしょう。
一方、ニューラルネットワークを学習させるためには正規化された出力層を使用する方が便利ですので、
(10)式で表されるAffine変換で求めた出力層のスコア値\(s_t\)を(9)式で表されるソフトマックス(Softmax)関数\(S(s_i)\)で正規化することが多いようです。
ここで、\(N\)は出力ベクトルの要素数ですので、(9)式の\(o_t\)は出力ベクトルの要素\(t\)が取り得る確率を表しています。
\[
o_t = S(s_t) = \frac{\exp(s_t)}{\displaystyle \sum_{ k = 0 }^{ K-1 }\exp(s_k)} \tag{9}
\]
\[
s_t = h_i^{(L-1)} w_{it}^{(L)} + b_t^{(L)} \tag{10}
\]
クロスエントロピー誤差とパープレキシティ
ニューラルネットワークを学習させるためには、ニューラルネットワークの出力結果が教師データ(正解)からどの程度乖離しているかを知る必要があります。
この乖離の程度を表す指標は損失関数(Loss Function)と呼ばれますが、ここでは損失関数として次式で表されるクロスエントロピー誤差(Cross Entropy Error)を使用します。
\[
E = \displaystyle - \sum_{ t = 0 }^{ T-1 } t_t \log(o_t) \tag{11}
\]
ここで、\(t_t\)は教師データベクトル、\(o_t\)は(9)式で表される正規化された出力ベクトル、\(\log\)はネイピア数\(e\)を底とする対数です。
一般的に、言語処理の分野では、入出力ベクトルや教師データベクトルとして正解要素のみ1で他の要素は0となるようなOne-hot表現が使用されますので、
クロスエントロピー誤差は、出力ベクトルの要素\(o_t\)が正解となる確率を対数で表現した指標と解釈できるでしょう。
さらに、次式で表される\(P\)をパープレキシティ(Perplexity)と呼びます。
\[
P = e^E \tag{12}
\]
パープレキシティは、要素\(o_t\)が正解となる確率の逆数を意味し、次に現れる単語の候補数が何個程度に絞り込めているかを表す指標と考えて良いでしょう。
クロスエントロピー誤差やパープレキシティは、図6に示すようなグラフで表されますが、要素\(o_t\)が正解となる確率が1に近づけば、クロスエントロピー誤差が0に近づき、
パープレキシティは1に近づいて行くことが分かります。
ニューラルネットワークの学習は、このクロスエントロピー誤差やパープレキシティを最小にするような重み\(w_{ij}^{(L)}\)やバイアス\(b_j^{(L)}\)を求めることに帰着されます。
なお、
RNNの実装 - バッチ処理に示した通り、
一般的に、言語モデルなどのニューラルネットワークの学習では大量のデータをまとめて処理するバッチ処理が行われますので、
クロスエントロピー誤差はバッチ数\(N\)の平均を取って次式で表されることになります。
そしてこの場合、パープレキシティは、次に現れる単語の候補数が平均して何個程度に絞り込めているかを表す指標と考えれば良いでしょう。
\[
E = \displaystyle - \frac{1}{N} \sum_{ N = 0 }^{ N-1 } \sum_{ t = 0 }^{ T-1 } t_{nt} \log(o_{nt}) \tag{13}
\]
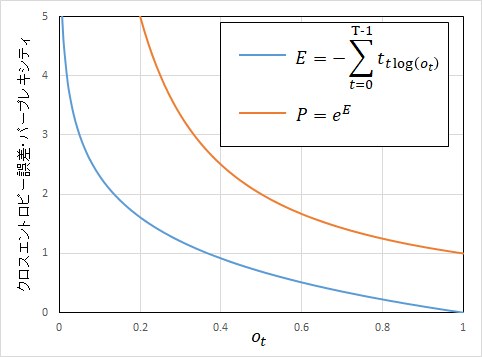
図6 クロスエントロピー誤差とパープレキシティ








-172.31.37.45。